《2025年暑假作业知识出版社七年级数学》

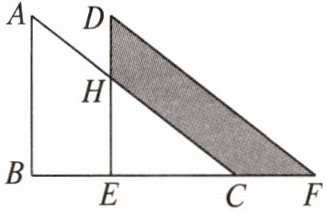
13. 如图,将直角三角形ABC沿直线BC向右平移后,到达三角形DEF的位置.若$ AB = 8cm $,$ BE = 4cm $,$ DH = 3cm $,求图中阴影部分的面积.

解 由平移的性质得，三角形 $ ABC $ 的面积等于三角形 $ DEF $ 的面积，$ AB = DE $，
则 $ HE = DE - DH = AB - DH = 8 - 3 = 5 \text{ cm} $。
阴影部分的面积等于梯形 $ ABEH $ 的面积，
$ S_{\text{阴影}} = \frac{1}{2}(AB + HE) \cdot BE = \frac{1}{2} × (8 + 5) × 4 = 26 \text{ cm}^2 $。

答案： 解 由平移的性质得，三角形 $ ABC $ 的面积等于三角形 $ DEF $ 的面积，$ AB = DE $，
则 $ HE = DE - DH = AB - DH = 8 - 3 = 5 \text{ cm} $。
阴影部分的面积等于梯形 $ ABEH $ 的面积，
$ S_{\text{阴影}} = \frac{1}{2}(AB + HE) \cdot BE = \frac{1}{2} × (8 + 5) × 4 = 26 \text{ cm}^2 $。