《2025年快乐假期暑假作业延边教育出版社七年级数学北师大版》

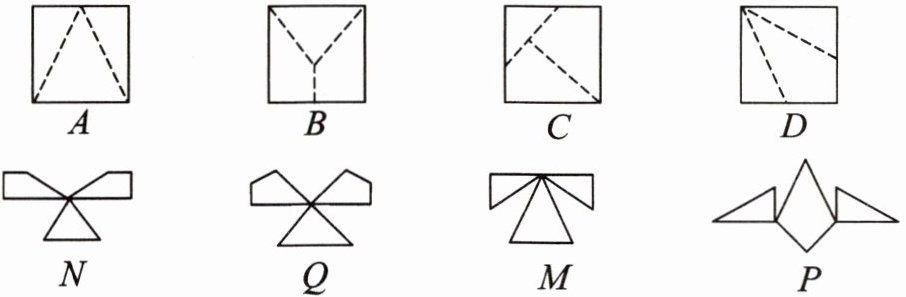
9. 如图所示,将编号为A,B,C,D的正方形沿图中的虚线剪开后,得到编号为N,Q,M,P的四个图形,试按照剪开前后图形的对应关系填空:A与M对应;B与N对应;C与Q对应;D与P对应.

答案： $M$，$N$，$Q$，$P$

10. 如图所示,已知在△ABC中,AB=AC=4,P是BC边上任意一点,PD⊥AB,PE⊥AC,点D,E为垂足.若△ABC的面积为6,则PD+PE的值是否能确定? 若能确定,请求出此值;若不能确定,请说明理由.

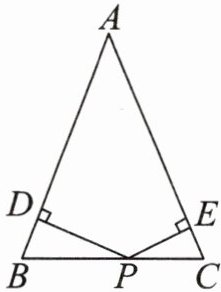
$PD + PE$的值能确定，且$PD + PE = 3$.
理由：连接$AP$，可得$S_{\triangle ABC} = S_{\triangle ABP} + S_{\triangle ACP}$.
因为$PD\perp AB$于点$D$，$PE\perp AC$于点$E$，$AB = AC = 4$，$\triangle ABC$的面积为6，
所以$6 = \frac{1}{2}× 4× PD + \frac{1}{2}× 4× PE = 2(PD + PE)$，所以$PD + PE = 3$.

答案： $PD + PE$的值能确定，且$PD + PE = 3$.
理由：连接$AP$，可得$S_{\triangle ABC} = S_{\triangle ABP} + S_{\triangle ACP}$.
因为$PD\perp AB$于点$D$，$PE\perp AC$于点$E$，$AB = AC = 4$，$\triangle ABC$的面积为6，
所以$6 = \frac{1}{2}\times 4\times PD + \frac{1}{2}\times 4\times PE = 2(PD + PE)$，所以$PD + PE = 3$.

11. 如图所示,△ABN≌△ACM,∠B和∠C是对应角,AB与AC是对应边,写出其他对应边和对应角.
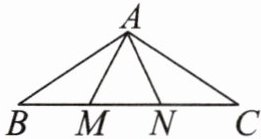
其他对应边：AN与AM，BN与CM；其他对应角：∠BAN=∠CAM，∠ANB=∠AMC.

答案： 因为$\triangle ABN\cong\triangle ACM$，$\angle B$和$\angle C$是对应角，$AB$与$AC$是对应边，
所以对应边：$AN$与$AM$，$BN$与$CM$；
对应角：$\angle BAN = \angle CAM$，$\angle ANB = \angle AMC$.