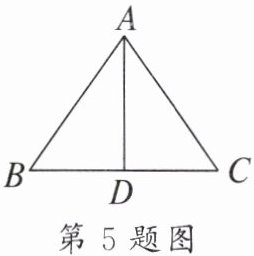
5. 如图,在$\triangle ABC$中,$AB=AC$,点D为BC的中点,$∠BAD=35^{\circ }$,则$∠C$的度数为____。

答案:
5. $55^{\circ}$
6. 如果一个三角形是轴对称图形,且有一个角为$60^{\circ }$,那么这个三角形是____,它有____条对称轴。
答案:
6. 等边三角形 3
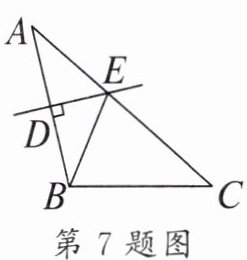
7. 如图,在$\triangle ABC$中,$AC=10$,$BC=6$,AB的垂直平分线交AB于点D,交AC于点E,则$\triangle BCE$的周长是____。

答案:
7. 16
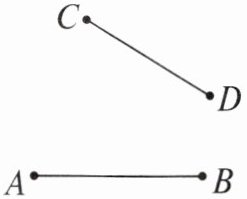
8. 如图,已知线段AB和CD,用尺规作一点,使它到AB和CD的两个端点的距离分别相等。

答案:
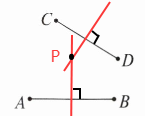
分别作线段$AB$和$CD$的垂直平分线,两垂直平分线的交点$P$即为所求作的点($P$点有$1$个或没有,取决于两垂直平分线是否相交)。

分别作线段$AB$和$CD$的垂直平分线,两垂直平分线的交点$P$即为所求作的点($P$点有$1$个或没有,取决于两垂直平分线是否相交)。
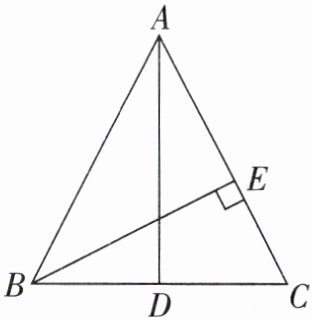
9. 如图,在$\triangle ABC$中,$AB=AC$,AD是BC边上的中线,$BE⊥AC$于点E。试说明$∠CBE=∠BAD$。

答案:
【解析】:
因为$AB = AC$,$AD$是$BC$边上的中线,根据等腰三角形三线合一的性质,所以$AD⊥BC$,$∠BAD = ∠CAD$(等腰三角形底边上的中线、底边上的高、顶角平分线三线合一)。
又因为$BE⊥AC$,所以$∠BEC = ∠ADC = 90^{\circ}$。
在$\triangle BEC$中,$∠CBE+∠C = 90^{\circ}$;在$\triangle ADC$中,$∠CAD + ∠C = 90^{\circ}$。
根据同角的余角相等,所以$∠CBE = ∠CAD$。
又因为$∠BAD = ∠CAD$,所以$∠CBE = ∠BAD$。
【答案】:$∠CBE = ∠BAD$
因为$AB = AC$,$AD$是$BC$边上的中线,根据等腰三角形三线合一的性质,所以$AD⊥BC$,$∠BAD = ∠CAD$(等腰三角形底边上的中线、底边上的高、顶角平分线三线合一)。
又因为$BE⊥AC$,所以$∠BEC = ∠ADC = 90^{\circ}$。
在$\triangle BEC$中,$∠CBE+∠C = 90^{\circ}$;在$\triangle ADC$中,$∠CAD + ∠C = 90^{\circ}$。
根据同角的余角相等,所以$∠CBE = ∠CAD$。
又因为$∠BAD = ∠CAD$,所以$∠CBE = ∠BAD$。
【答案】:$∠CBE = ∠BAD$
查看更多完整答案,请扫码查看


