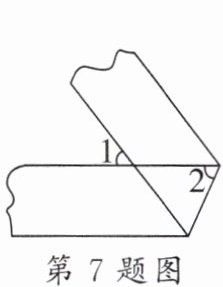
7. 如图,将一条两边都互相平行的纸带进行折叠,设$∠1=a^{\circ}$,则$∠2=$______(用含$a$的代数式表示)。

答案:
$ 90^{\circ}-\frac{a}{2} $
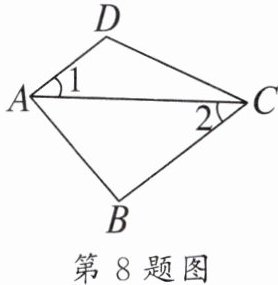
8. 如图,若$∠1=∠2$,$∠DAB=83^{\circ}$,则$∠B$的度数为______。

答案:
$ 97^{\circ} $
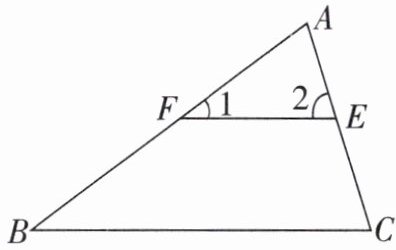
9. 如图,如果$∠1=36^{\circ}$,$∠C=74^{\circ}$,$∠B=36^{\circ}$,求$∠2$的度数。

答案:
$ \angle 2=74^{\circ} $。
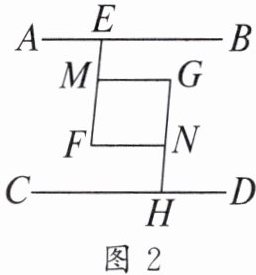
10. 中国汉字博大精深,方块文字智慧灵秀、奥妙无穷。图1是一个“互”字,可以抽象成图2所示的几何图形,其中$AB// CD$,$MG// FN$,点$E$,$M$,$F$在同一直线上,点$G$,$N$,$H$在同一直线上,且$∠AEF=∠GHD$。试说明$∠EFN=∠G$。(提示:延长$EF$交$CD$于点$P$)



答案:
【解析】:
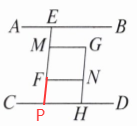
- 延长$EF$交$CD$于点$P$。
- 因为$AB// CD$,根据“两直线平行,同位角相等”,可得$\angle AEF = \angle EPD$。
- 又因为$\angle AEF=\angle GHD$,所以$\angle EPD=\angle GHD$。
- 根据“同位角相等,两直线平行”,由$\angle EPD=\angle GHD$可推出$EP// GH$。
- 因为$MG// FN$,根据“两直线平行,同位角相等”,$\angle EFN$与$\angle EPD$是同位角($FN// MG$,$EP// GH$,通过平行线的传递性等相关性质转化),$\angle G$与$\angle EPD$是同位角($EP// GH$),所以$\angle EFN=\angle G$。
【答案】:$\angle EFN=\angle G$
【解析】:

- 延长$EF$交$CD$于点$P$。
- 因为$AB// CD$,根据“两直线平行,同位角相等”,可得$\angle AEF = \angle EPD$。
- 又因为$\angle AEF=\angle GHD$,所以$\angle EPD=\angle GHD$。
- 根据“同位角相等,两直线平行”,由$\angle EPD=\angle GHD$可推出$EP// GH$。
- 因为$MG// FN$,根据“两直线平行,同位角相等”,$\angle EFN$与$\angle EPD$是同位角($FN// MG$,$EP// GH$,通过平行线的传递性等相关性质转化),$\angle G$与$\angle EPD$是同位角($EP// GH$),所以$\angle EFN=\angle G$。
【答案】:$\angle EFN=\angle G$
查看更多完整答案,请扫码查看


