《2025年暑假作业兰州大学出版社七年级数学北师大版》

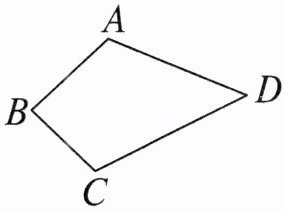
10. 某地有四个汽车停车场，分别位于如图所示的四边形$ABCD$的四个顶点处。现在要建立一个汽车维修站，请你利用“三角形任意两边之和大于第三边”的性质，在四边形$ABCD$的内部找一点$O$，使点$O$到$A$，$B$，$C$，$D$四点的距离之和最小，并说明理由。

答案：

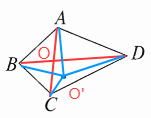
连接 AC、BD，它们的交点 O 即为所求。
理由：任取四边形内一点 $O'$（非 $AC$、$BD$ 交点），连接 $O'A$、$O'B$、$O'C$、$O'D$。根据“三角形任意两边之和大于第三边”，$O'A + O'C > AC$，$O'B + O'D > BD$，即 $O'A + O'B + O'C + O'D > AC + BD = OA + OB + OC + OD$，所以 $AC$、$BD$ 交点 $O$ 到 $A$、$B$、$C$、$D$ 四点距离之和最小。

11. 在$\triangle ABC$中，$\angle B$，$\angle C$的平分线相交于点$P$，设$\angle A = x^{\circ}$，用含$x$的代数式表示$\angle BPC$的度数，下列正确的是（ ）
A. $90^{\circ} + \frac{1}{2}x^{\circ}$
B. $90^{\circ} - \frac{1}{2}x^{\circ}$
C. $90^{\circ} + 2x^{\circ}$
D. $90^{\circ} + x^{\circ}$

答案： A

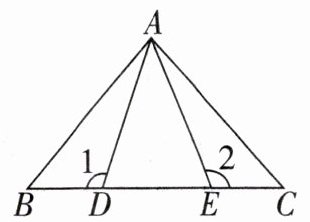
12. 如图，$AD = AE$，$BD = CE$，$\angle 1 = \angle 2 = 110^{\circ}$，$\angle BAE = 60^{\circ}$，则$\angle CAE =$______。

答案： $ 20 ^ { \circ } $