《2025年暑假作业兰州大学出版社七年级数学北师大版》

13. 请认真观察图形，解答下列问题。

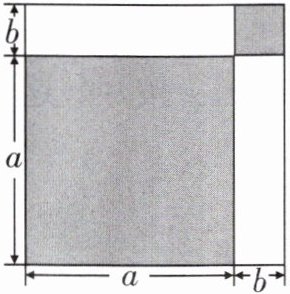
（1）根据图中所标注的数据，用两种方法表示两个阴影部分的面积之和；
（2）由（1）你能得到怎样的等量关系？请用等式表示；
（3）如果$a$，$b(a ＞ b)$满足$a^{2} + b^{2} = 53$，$ab = 14$，求出$a + b$和$a^{4} - b^{4}$的值。

答案：
(1) $a^{2}+b^{2}$，$(a + b)^{2}-2ab$；
(2) $a^{2}+b^{2} =(a + b)^{2}-2ab$；
(3) $(a + b)^{2}=a^{2}+b^{2}+2ab = 81$，因为 $a ＞ b ＞ 0$，所以 $a + b = 9$。$(a - b)^{2}=a^{2}+b^{2}-2ab = 25$。因为 $a ＞b$，所以 $a - b = 5$，所以 $a^{4}-b^{4}=(a^{2}+b^{2})(a + b)(a - b)=2385$。