《2025年暑假作业兰州大学出版社七年级数学北师大版》

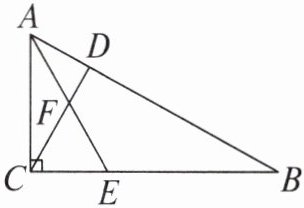
13. 如图，在$Rt\triangle ABC$中，$\angle ACB = 90^{\circ}$，点$D$是$AB$上一点，且$\angle ACD = \angle B$。
（1）试说明$CD \perp AB$；
（2）在（1）中作$\triangle ABC$的角平分线$AE$，交$CD$于点$F$，试判断$\angle AEC$和$\angle CFE$的数量关系，并说明理由。

答案：
(1)因为∠ACB=90° ，所以∠ACD+∠BCD=90 ° 。又因为∠ACD=∠B，等量代换可得∠B+∠BCD=90 ° 。在△BCD中，根据三角形内角和为180° ，可得∠BDC=180 ° −(∠B+∠BCD)=90° ，所以CD⊥AB 。
(2) $ \angle AEC = \angle CFE $。
因为$AE$是角平分线，所以$\angle CAE=\angle BAE$。
由$\angle ACB=90^{\circ}$，$CD\perp AB$，可得$\angle CAE+\angle AEC=90^{\circ}$，$\angle BAE+\angle AFD=90^{\circ}$。
根据等角的余角相等，所以$\angle AEC=\angle AFD$。
又因为$\angle AFD=\angle CFE$（对顶角相等），所以$\angle AEC=\angle CFE$。