《2025年暑假作业兰州大学出版社七年级数学北师大版》

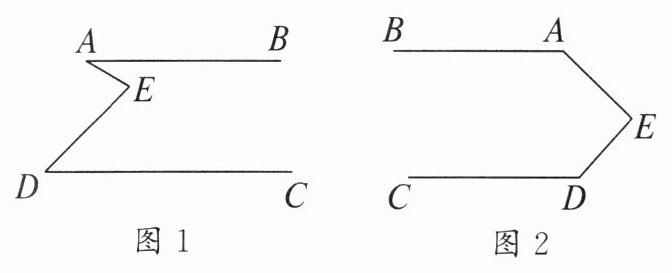
20. （14分）已知$AB// CD$，在$AB$，$CD$之间任取一点$E$，连接$EA$，$ED$。
（1）如图1，若$∠A=30^{\circ}$，$∠D=45^{\circ}$，求$∠E$的度数；
（2）如图2，猜想$∠A$，$∠AED$，$∠D$之间的数量关系，并说明理由。

答案：

解：
(1)过点$E$作$EF// AB$。

因为$AB// CD$，$EF// AB$，根据平行公理的推论：如果两条直线都与第三条直线平行，那么这两条直线也互相平行，所以$EF// CD$。

根据平行线的性质：两直线平行，内错角相等。

因为$EF// AB$，$\angle A = 30^{\circ}$，所以$\angle AEF=\angle A = 30^{\circ}$。

因为$EF// CD$，$\angle D = 45^{\circ}$，所以$\angle DEF=\angle D = 45^{\circ}$。

则$\angle AED=\angle AEF+\angle DEF=30^{\circ}+45^{\circ}=75^{\circ}$。

(2)猜想：$\angle A+\angle D+\angle AED=360°$。

理由如下：

过点$E$作$EF// AB$。

因为$AB// CD$，$EF// AB$，所以$EF// CD$（平行公理的推论）。

因为$EF// AB$，所以$\angle A+\angle AEF=180°$（两直线平行，同旁内角互补）。

因为$EF// CD$，所以$\angle D+\angle DEF=180°$（两直线平行，同旁内角互补）。

又因为$\angle AED=\angle AEF+\angle DEF$，所以$\angle A+\angle D+\angle AED=360°$。

综上，$(1)$$\angle E = 75^{\circ}$；$(2)$$\angle A+\angle D+\angle AED=360°$ 。