2025年暑假课程练习南方出版社五年级数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假课程练习南方出版社五年级数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 在$\frac {2}{5}$、$\frac {5}{4}$和$\frac {8}{9}$这三个分数中,分数单位最小的数是(
A. $\frac {2}{5}$
B. $\frac {5}{4}$
C. $\frac {8}{9}$
C
)。A. $\frac {2}{5}$
B. $\frac {5}{4}$
C. $\frac {8}{9}$
答案:
C
2. 将下列图形绕着各自的中心旋转$120^{\circ }$后,不能与原来的图形重合的是(
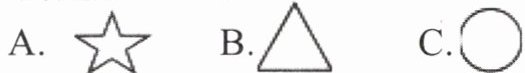
A
)。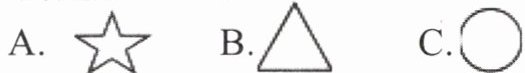
答案:
A
3. $a÷b=c$($a$、$b$和$c$都不为$0$),$a$和$b$的最小公倍数是(
A. $a$
B. $b$
C. $c$
A
)。A. $a$
B. $b$
C. $c$
答案:
A
4. 如下图,线段$OA$绕点$O$逆时针旋转$90^{\circ }$后得到的线段是(
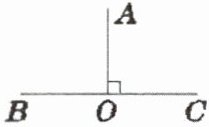
A. $OC$
B. $OB$
C. $OA$
B
)。
A. $OC$
B. $OB$
C. $OA$
答案:
B
5. 将下面的图形绕点$O$顺时针旋转$90^{\circ }$,得到的图形是(
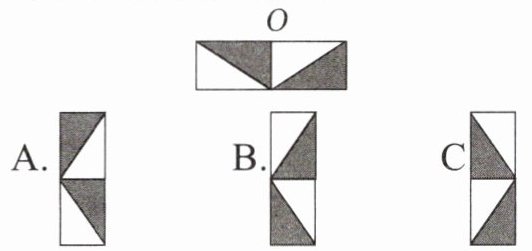
C
)。
答案:
C
1. 东东把一张纸条连续对折$3$次,这时每段占这张纸条的$\frac{(
1
)}{(8
)}$。
答案:
$\frac{1}{8}$
2. 在下面的括号里填上适当的分数。
$13cm=$(
$400g=$(
$1500mL=$(
$1$时$20$分=(
$13cm=$(
$\frac{13}{100}$
)$m$$400g=$(
$\frac{2}{5}$
)$kg$$1500mL=$(
$\frac{3}{2}$
)$L$$1$时$20$分=(
$\frac{4}{3}$
)时
答案:
1.$\frac{13}{100}$ 2.$\frac{2}{5}$ 3.$\frac{3}{2}$ 4.$\frac{4}{3}$
3. 在$〇$内填上“$>$”“$<$”或“$=$”。
$\frac {4}{9}〇$
$\frac {2}{7}〇$
$\frac {10}{3}〇$
$\frac {6}{9}〇$
$\frac {1}{8}〇$
$\frac {7}{6}〇$
$\frac {4}{9}〇$
$<$
$\frac {5}{9}$$\frac {2}{7}〇$
$<$
$\frac {2}{5}$$\frac {10}{3}〇$
$>$
$\frac {13}{4}$$\frac {6}{9}〇$
$=$
$\frac {8}{12}$$\frac {1}{8}〇$
$=$
$0.125$$\frac {7}{6}〇$
$>$
$\frac {8}{7}$
答案:
$\lt$ $\lt$ $\gt$ $=$ $=$ $\gt$
三、把下面各小数化成分数,分数化成小数。(不能化成有限小数的,保留两位小数)
$0.48$
$4.25$
$\frac {27}{50}$
$\frac {24}{300}$
$\frac {8}{12}$
$\frac {15}{14}$
$0.48$
$4.25$
$\frac {27}{50}$
$\frac {24}{300}$
$\frac {8}{12}$
$\frac {15}{14}$
答案:
【解析】:
1. 将$0.48$化成分数,因为$0.48=\frac{48}{100}$,分子分母同时除以$4$进行约分,$\frac{48\div4}{100\div4}=\frac{12}{25}$。
2. 把$4.25$化成分数,$4.25 = 4+\frac{25}{100}$,$\frac{25}{100}$约分后为$\frac{1}{4}$,所以$4.25 = 4\frac{1}{4}=\frac{17}{4}$。
3. 把$\frac{27}{50}$化成小数,用分子除以分母,$27\div50 = 0.54$。
4. 对于$\frac{24}{300}$,先约分,分子分母同时除以$12$得$\frac{2}{25}$,再化成小数,$2\div25 = 0.08$。
5. 计算$\frac{8}{12}$,先约分,分子分母同时除以$4$得$\frac{2}{3}$,$2\div3\approx0.67$(保留两位小数)。
6. 计算$\frac{15}{14}$,$15\div14\approx1.07$(保留两位小数)。
【答案】:$\frac{12}{25}$;$\frac{17}{4}$;$0.54$;$0.08$;$0.67$;$1.07$
1. 将$0.48$化成分数,因为$0.48=\frac{48}{100}$,分子分母同时除以$4$进行约分,$\frac{48\div4}{100\div4}=\frac{12}{25}$。
2. 把$4.25$化成分数,$4.25 = 4+\frac{25}{100}$,$\frac{25}{100}$约分后为$\frac{1}{4}$,所以$4.25 = 4\frac{1}{4}=\frac{17}{4}$。
3. 把$\frac{27}{50}$化成小数,用分子除以分母,$27\div50 = 0.54$。
4. 对于$\frac{24}{300}$,先约分,分子分母同时除以$12$得$\frac{2}{25}$,再化成小数,$2\div25 = 0.08$。
5. 计算$\frac{8}{12}$,先约分,分子分母同时除以$4$得$\frac{2}{3}$,$2\div3\approx0.67$(保留两位小数)。
6. 计算$\frac{15}{14}$,$15\div14\approx1.07$(保留两位小数)。
【答案】:$\frac{12}{25}$;$\frac{17}{4}$;$0.54$;$0.08$;$0.67$;$1.07$
四、动手操作。
1. 画出三角形绕点$O$逆时针旋转$90^{\circ }$后的图形$A$。
2. 画出将图形$A$向右平移$2$格后的图形$B$。

1. 画出三角形绕点$O$逆时针旋转$90^{\circ }$后的图形$A$。
按照旋转性质,确定三角形除$O$点外两顶点绕$O$逆时针旋转$90^{\circ }$后的位置,连接$O$点与这两个新顶点得到图形$A$
2. 画出将图形$A$向右平移$2$格后的图形$B$。
将图形$A$各顶点向右平移$2$格,依次连接平移后顶点得到图形$B$

答案:
【解析】:
1. 对于三角形绕点$O$逆时针旋转$90^{\circ}$:
旋转的性质是图形上的每一点都绕旋转中心沿相同方向转动相同的角度,对应点到旋转中心的距离相等。
先确定三角形除$O$点外的两个顶点绕点$O$逆时针旋转$90^{\circ}$后的位置。假设原三角形的一个顶点$P$(非$O$点),以$O$为中心,将$OP$线段逆时针旋转$90^{\circ}$,得到新的顶点$P'$。同理找到另一个顶点旋转后的位置,然后连接这三个顶点($O$点不变,另外两个旋转后的顶点)得到图形$A$。
2. 对于图形$A$向右平移$2$格:
平移的性质是图形上的所有点都按照某个方向作相同距离的移动。
把图形$A$的每个顶点都向右平移$2$格,然后依次连接这些平移后的顶点,得到图形$B$。
【答案】:按照上述方法画出图形$A$和图形$B$(由于是动手操作题,无法用文字精确描述图形,学生根据旋转和平移的性质在方格纸上画出即可)。
1. 对于三角形绕点$O$逆时针旋转$90^{\circ}$:
旋转的性质是图形上的每一点都绕旋转中心沿相同方向转动相同的角度,对应点到旋转中心的距离相等。
先确定三角形除$O$点外的两个顶点绕点$O$逆时针旋转$90^{\circ}$后的位置。假设原三角形的一个顶点$P$(非$O$点),以$O$为中心,将$OP$线段逆时针旋转$90^{\circ}$,得到新的顶点$P'$。同理找到另一个顶点旋转后的位置,然后连接这三个顶点($O$点不变,另外两个旋转后的顶点)得到图形$A$。
2. 对于图形$A$向右平移$2$格:
平移的性质是图形上的所有点都按照某个方向作相同距离的移动。
把图形$A$的每个顶点都向右平移$2$格,然后依次连接这些平移后的顶点,得到图形$B$。
【答案】:按照上述方法画出图形$A$和图形$B$(由于是动手操作题,无法用文字精确描述图形,学生根据旋转和平移的性质在方格纸上画出即可)。
查看更多完整答案,请扫码查看


