《2025年暑假课程练习南方出版社五年级数学》

1. 一个长 14 cm，宽 8 cm，高 6 cm 的长方体的六个面中最大的面的面积是（1.12）$dm^{2}$，最小的面的面积是（0.48）$dm^{2}$。

答案： 1. $1.12$ $0.48$

2. 棱长为 6 dm 的正方体木块可以切成（27）个棱长为 2 dm 的正方体。

答案： 27

3. 一个长方体长是 9 cm，宽是 7 cm，高是 5 cm。把它切成一个尽可能大的正方体，这个正方体的棱长是（5）cm。

答案： 5

4. 一个正方体的棱长是 3 dm，它的棱长之和是（36）dm，表面积是（54）$dm^{2}$，体积是（27）$dm^{3}$。

答案： 36 54 27

二、判断。(正确的在括号里画“√”，错误的画“×”)
1. 所有的质数都是奇数。（×）
2. 若一个长方体的左面是正方形，则它的右面也是正方形。（√）
3. 用 12 个棱长是 1 cm 的小正方体木块摆成不同形状的长方体，它们的体积不一定都是 12$cm^{3}$。（×）
4. 体积是 1$dm^{3}$的物体，不一定是棱长为 1 dm 的正方体。（√）

答案： 1.× 2.√ 3.× 4.√

1. 张叔叔要制作一个长方体框架（如图），至少需要多少米的木条？（单位：m）

（25.2）

答案： 【解析】：本题可根据长方体棱长总和公式来计算所需木条长度，长方体棱长总和$=$（长$+$宽$+$高）$\times4$。
已知长方体框架的长是$2.5m$、宽是$1.8m$、高是$2m$，将其代入公式可得：$(2.5 + 1.8 + 2)\times4$
先计算括号内的值：$2.5+1.8 + 2=6.3$（$m$）
再计算乘法：$6.3\times4 = 25.2$（$m$）
【答案】：$25.2$

2. 一块面积为 6.5$dm^{2}$的正方形木板如图竖直放置，现让这块木板向右平移 4.3 dm，它扫过的空间形成的立体图形体积是多少立方分米？

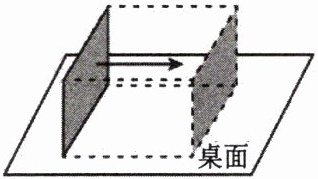
27.95

答案： 【解析】：本题可根据平移的性质确定扫过的空间形成的立体图形为长方体，再根据长方体的体积公式求解。
- **步骤一：分析扫过的空间形成的立体图形**
根据平移的性质可知，正方形木板向右平移后扫过的空间形成的立体图形是一个长方体。
该长方体的底面积就是正方形木板的面积$6.5dm^{2}$，高为平移的距离$4.3dm$。
- **步骤二：计算长方体的体积**
根据长方体的体积公式$V = S\times h$（其中$V$为长方体体积，$S$为长方体底面积，$h$为长方体的高），将$S = 6.5dm^{2}$，$h = 4.3dm$代入公式可得：
$V=6.5\times4.3 = 27.95(dm^{3})$
【答案】：$27.95$

3. 一个棱长是 1.2 dm 的正方体鱼缸，里面装满水。把水全部倒入一个长为 1.6 dm、宽为 1 dm 的长方体鱼缸里，水有多深？

答案： 【解析】：本题可先根据正方体的体积公式$V = a^3$（其中$V$为正方体体积，$a$为正方体棱长）求出正方体鱼缸中水的体积，因为水的体积不变，再将水倒入长方体鱼缸中，根据长方体的体积公式$V = abh$（其中$V$为长方体体积，$a$为长方体的长，$b$为长方体的宽，$h$为长方体的高），可得$h = V\div(ab)$，进而求出水在长方体鱼缸中的深度。
计算正方体鱼缸中水的体积：
已知正方体鱼缸棱长$a = 1.2dm$，根据正方体体积公式可得水的体积$V = 1.2^3 = 1.2×1.2×1.2 = 1.728(dm^3)$。
计算水在长方体鱼缸中的深度：
已知长方体鱼缸长$a = 1.6dm$、宽$b = 1dm$，水的体积$V = 1.728dm^3$，根据长方体体积公式的变形可得水的深度$h = 1.728\div(1.6×1) = 1.728\div1.6 = 1.08(dm)$。
【答案】：1.08dm