《2025年新课堂暑假生活七年级数学》

8. 解方程组：
(1) $ \left\{ \begin{array} { l } { 3 x + y = 82, } \\ { 10 x - 11 y = 87 ; } \end{array} \right. $
解：$\begin{cases}x = 23\\y = 13\end{cases}$
(2) $ \left\{ \begin{array} { l } { x - 2 = 2 ( y - 1 ), } \\ { 2 ( x - 2 ) + ( y - 1 ) = 5. } \end{array} \right. $
解：$\begin{cases}x = 4\\y = 2\end{cases}$

答案： 【解析】：
(1)
对于方程组$\begin{cases}3x + y = 82&(a)\\10x - 11y = 87&(b)\end{cases}$
由$(a)$式可得$y = 82 - 3x$ $(c)$
将$(c)$式代入$(b)$式得：
$10x-11(82 - 3x)=87$
去括号得：$10x-902 + 33x = 87$
移项得：$10x+33x=87 + 902$
合并同类项得：$43x=989$
解得：$x = 23$
把$x = 23$代入$(c)$式得：$y=82-3×23=82 - 69 = 13$
(2)
对于方程组$\begin{cases}x - 2 = 2(y - 1)&(d)\\2(x - 2)+(y - 1)=5&(e)\end{cases}$
设$m=x - 2$，$n=y - 1$，则原方程组可化为$\begin{cases}m = 2n&(f)\\2m + n = 5&(g)\end{cases}$
将$(f)$式代入$(g)$式得：$2×2n+n = 5$
即$4n + n = 5$
$5n = 5$
解得$n = 1$
把$n = 1$代入$(f)$式得：$m = 2×1=2$
因为$m=x - 2$，$n=y - 1$
所以$\begin{cases}x-2 = 2\\y - 1 = 1\end{cases}$
解得$\begin{cases}x=4\\y = 2\end{cases}$
【答案】：
(1)$\begin{cases}x = 23\\y = 13\end{cases}$；
(2)$\begin{cases}x = 4\\y = 2\end{cases}$

9. 如图,直线 $ l $ 和 $ m $ 相交于点 $ C $,$ \angle C = \angle \beta $,$ AP $,$ BP $ 交于点 $ P $,且 $ \angle P A C = \angle \alpha $,$ \angle P B C = \angle \gamma $。求证：$ \angle A P B = \angle \alpha + \angle \beta + \angle \gamma $。


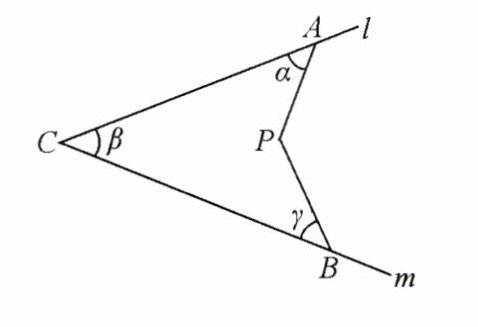
过点$P$作$PF// l$，交$CB$于点$F$。
$\because PF// l$，$\therefore\angle APF = \angle PAC=\angle\alpha$（两直线平行，内错角相等）。
$\because\angle C=\angle\beta$，$PF// l$，$\therefore PF// m$（平行于同一条直线的两条直线互相平行）。
$\therefore\angle FPB=\angle PBC = \angle\gamma$（两直线平行，内错角相等）。
$\because\angle APB=\angle APF+\angle FPB+\angle\beta$，$\therefore\angle APB=\angle\alpha+\angle\beta+\angle\gamma$。

答案： 【解析】：
过点$P$作$PF// l$，交$CB$于点$F$。
因为$PF// l$，所以$\angle APF = \angle PAC=\angle\alpha$（两直线平行，内错角相等）。
又因为$l$和$m$相交于点$C$，$\angle C=\angle\beta$，$PF// l$，所以$PF// m$（平行于同一条直线的两条直线互相平行）。
则$\angle FPB=\angle PBC = \angle\gamma$（两直线平行，内错角相等）。
而$\angle APB=\angle APF+\angle FPB+\angle\beta$，把$\angle APF = \angle\alpha$，$\angle FPB=\angle\gamma$代入可得$\angle APB=\angle\alpha+\angle\beta+\angle\gamma$。
【答案】：
过点$P$作$PF// l$，交$CB$于点$F$。
$\because PF// l$，$\therefore\angle APF = \angle PAC=\angle\alpha$（两直线平行，内错角相等）。
$\because\angle C=\angle\beta$，$PF// l$，$\therefore PF// m$（平行于同一条直线的两条直线互相平行）。
$\therefore\angle FPB=\angle PBC = \angle\gamma$（两直线平行，内错角相等）。
$\because\angle APB=\angle APF+\angle FPB+\angle\beta$，$\therefore\angle APB=\angle\alpha+\angle\beta+\angle\gamma$。

10. 某校七年级共有 240 名学生,检测每名学生的视力后得到如下数据：
视力从低到高分为 1, 2, 3, 4, 5 级,试用合适的统计图表示上述信息。用条形统计图表示

答案： 【解析】：因为要表示不同视力等级（不同类别）的人数情况，而条形统计图的特点是可以清楚地表明各种数量的多少，所以用条形统计图来表示上述信息较为合适。
【答案】：用条形统计图表示。