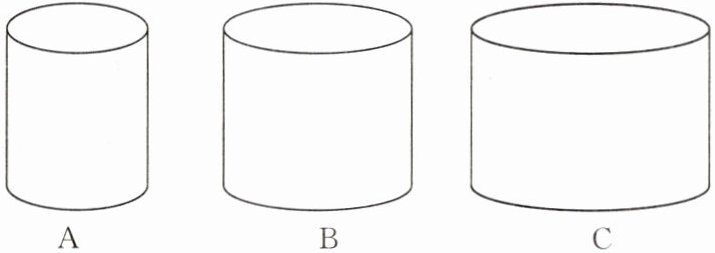
12. 如图,有高度相同的A,B,C三只圆柱形杯子,A,B两只杯子盛满了水,小颖把A,B两只杯子中的水全部倒进C杯中,C杯恰好装满,小颖测量得A,B两只杯子底面圆的半径分别是3cm和4cm,你能求出C杯底面圆的半径是多少吗?(杯子的厚度忽略不计;圆柱的体积公式是$V= πr^{2}h$,其中$r$是圆柱底面半径)

5cm
答案:
【解析】:设三只杯子的高度均为$h cm$,$C$杯底面圆的半径是$R cm$。
根据圆柱体积公式$V = \pi r^{2}h$,$A$杯体积$V_{A}=\pi×3^{2}× h = 9\pi h$,$B$杯体积$V_{B}=\pi×4^{2}× h = 16\pi h$。
因为$A$、$B$两杯的水全部倒进$C$杯恰好装满,所以$V_{A}+V_{B}=V_{C}$,即$9\pi h + 16\pi h=\pi R^{2}h$。
两边同时除以$\pi h$($h\neq0$),得到$9 + 16 = R^{2}$,$R^{2}=25$,解得$R = 5$($R=-5$舍去,因为半径为正数)。
【答案】:$5cm$
根据圆柱体积公式$V = \pi r^{2}h$,$A$杯体积$V_{A}=\pi×3^{2}× h = 9\pi h$,$B$杯体积$V_{B}=\pi×4^{2}× h = 16\pi h$。
因为$A$、$B$两杯的水全部倒进$C$杯恰好装满,所以$V_{A}+V_{B}=V_{C}$,即$9\pi h + 16\pi h=\pi R^{2}h$。
两边同时除以$\pi h$($h\neq0$),得到$9 + 16 = R^{2}$,$R^{2}=25$,解得$R = 5$($R=-5$舍去,因为半径为正数)。
【答案】:$5cm$
查看更多完整答案,请扫码查看


