1. 已知:如图,$AB// CD,BC// AD,∠3= ∠4.$
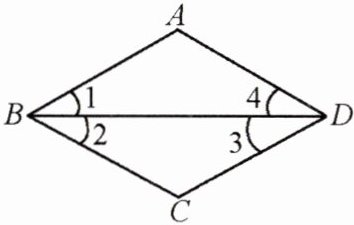
求证:$∠1= ∠2.$
证明:$\because AB// CD$(
$\therefore$
$\because BC// AD$(已知),
$\therefore$
$\because ∠3= ∠4$(

求证:$∠1= ∠2.$
证明:$\because AB// CD$(
已知
),$\therefore$
$\angle 1$
=$\angle 3$
(两直线平行,内错角相等
).$\because BC// AD$(已知),
$\therefore$
$\angle 2$
=$\angle 4$
(两直线平行,内错角相等
).$\because ∠3= ∠4$(
已知
),$\therefore ∠1= ∠2$(等量代换
).
答案:
$\angle 1$,$\angle 3$,两直线平行,内错角相等;
$\angle 2$,$\angle 4$,两直线平行,内错角相等;
已知,等量代换。
$\angle 2$,$\angle 4$,两直线平行,内错角相等;
已知,等量代换。
2. 如图,以下推理正确的是 (
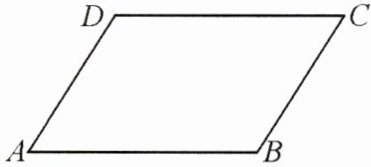
A.若$∠A+∠B= 180^{\circ }$,则$AD// BC$
B.若$∠A+∠B= 180^{\circ }$,则$AB// CD$
C.若$∠A= ∠C$,则$AB// CD$
D.若$∠A= ∠C$,则$AD// BC$
A
)
A.若$∠A+∠B= 180^{\circ }$,则$AD// BC$
B.若$∠A+∠B= 180^{\circ }$,则$AB// CD$
C.若$∠A= ∠C$,则$AB// CD$
D.若$∠A= ∠C$,则$AD// BC$
答案:
2. A
3. 如图,面积为$12cm^{2}$的三角形 ABC 沿 BC 方向平移至三角形 DEF 的位置,平移的距离是边 BC 长的两倍,则四边形 ACED 的面积为(

A.$24cm^{2}$
B.$36cm^{2}$
C.$48cm^{2}$
D.无法确定
B
)
A.$24cm^{2}$
B.$36cm^{2}$
C.$48cm^{2}$
D.无法确定
答案:
3. B
4. 若两条平行直线被第三条直线所截得的 8 个角中有 1 个角的度数已知,则 (
A.能求出其余 3 个角的度数
B.能求出其余 5 个角的度数
C.能求出其余 6 个角的度数
D.能求出其余 7 个角的度数
D
)A.能求出其余 3 个角的度数
B.能求出其余 5 个角的度数
C.能求出其余 6 个角的度数
D.能求出其余 7 个角的度数
答案:
4. D
查看更多完整答案,请扫码查看


