1.如图,$△ABC的一边AB是\odot O$的直径,请你添加一个条件,使$BC是\odot O$的切线,你所添加的条件为
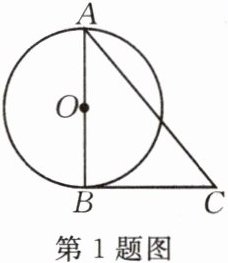
$∠ABC=90^{\circ }$
.
答案:
$∠ABC=90^{\circ }$
2.如图,$AB是\odot O$的直径,点$C在\odot O$上,$AE是\odot O$的切线,$A$为切点,连接$BC并延长交AE于点D$,若$∠AOC= 80^{\circ }$,则$∠ADB$的度数为(
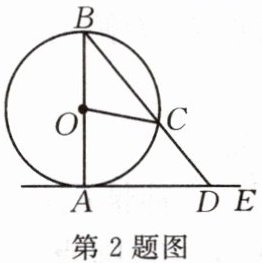
A.$40^{\circ }$
B.$50^{\circ }$
C.$60^{\circ }$
D.$20^{\circ }$
B
)
A.$40^{\circ }$
B.$50^{\circ }$
C.$60^{\circ }$
D.$20^{\circ }$
答案:
B
3.如图,在$\odot O$中,$AB$为直径,$BC$为弦,$CD$为切线,连接$OC$,若$∠BCD= 50^{\circ }$,则$∠AOC$的度数为(

A.$40^{\circ }$
B.$50^{\circ }$
C.$80^{\circ }$
D.$100^{\circ }$
C
)
A.$40^{\circ }$
B.$50^{\circ }$
C.$80^{\circ }$
D.$100^{\circ }$
答案:
C
4.如图,等腰直角三角形$ABC$中,$AB= AC= 8$,$O为BC$的中点,以$O为圆心作半圆与AB$,$AC$都相切,切点分别为$D$,$E$,则$\odot O$的半径为(
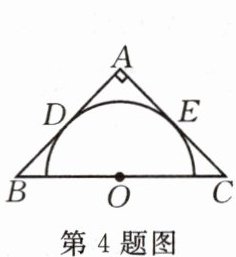
A.8
B.6
C.5
D.4
D
)
A.8
B.6
C.5
D.4
答案:
D
5.如图,AB是$\odot O$的直径,O是圆心,BC与$\odot O$相切于B点,CO与$\odot O$相交于点D,且BC= 8,CD= 4,那么$\odot O$的半径是
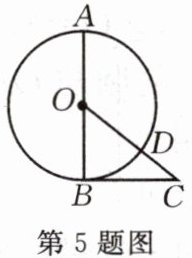
6
.
答案:
6
6.如图,$AB为\odot O$的直径,$EF切\odot O于点D$,过点$B作BH⊥EF于点H$,交$\odot O于点C$,连接$BD$.
(1)求证:$BD平分∠ABH$;
(2)如果$AB= 12$,$BC= 8$,求圆心$O到BC$的距离.

(1)求证:$BD平分∠ABH$;
(2)如果$AB= 12$,$BC= 8$,求圆心$O到BC$的距离.

答案:
(1)连接$OD$,$\because EF$是$\odot O$的切线,$OD⊥EF$,又$\because BH⊥EF$,$\therefore OD// BH$,$\therefore ∠ODB=∠DBH$,
$\because OD=OB$,$\therefore ∠ODB=∠OBD$,
$\therefore ∠OBD=∠DBH$,$\therefore BD$平分$∠ABH$;
(2)过点$O$作$OG⊥BC$于点$G$,则$BG=CG=4$,在$Rt\triangle OBG$中,$OG=\sqrt {OB^{2}-BG^{2}}=\sqrt {6^{2}-4^{2}}=2\sqrt {5}$。
(1)连接$OD$,$\because EF$是$\odot O$的切线,$OD⊥EF$,又$\because BH⊥EF$,$\therefore OD// BH$,$\therefore ∠ODB=∠DBH$,
$\because OD=OB$,$\therefore ∠ODB=∠OBD$,
$\therefore ∠OBD=∠DBH$,$\therefore BD$平分$∠ABH$;
(2)过点$O$作$OG⊥BC$于点$G$,则$BG=CG=4$,在$Rt\triangle OBG$中,$OG=\sqrt {OB^{2}-BG^{2}}=\sqrt {6^{2}-4^{2}}=2\sqrt {5}$。
7.如图,$AB= AC$,以$AB为直径的\odot O交BC于D$,$DE⊥AC于E$.
(1)求证:$DE是\odot O$的切线;
(2)若$AB= 10$,$BC= 4\sqrt {5}$,求$OE$的长.

(1)求证:$DE是\odot O$的切线;
(2)若$AB= 10$,$BC= 4\sqrt {5}$,求$OE$的长.

答案:
(1)方法一:连接$OD$,证$∠B=∠ODB=∠C$,$\therefore OD// AC$,
$\therefore ∠ODE=90^{\circ }$,$\therefore DE$是$\odot O$的切线;
方法二:连接$OD$,$AD$,证$AD⊥BC$,$\because AB=AC$,$\therefore BD=CD$,$\because OA=OB$,$\therefore OD// AC$,……以下同方法一;
(2)连接$AD$,易证$BD=CD=2\sqrt {5}$,$\therefore AD=4\sqrt {5}$,
$\because AD\cdot CD=AC\cdot DE$,$\therefore DE=4$,
$\therefore OE=\sqrt {OD^{2}+DE^{2}}=\sqrt {41}$。
(1)方法一:连接$OD$,证$∠B=∠ODB=∠C$,$\therefore OD// AC$,
$\therefore ∠ODE=90^{\circ }$,$\therefore DE$是$\odot O$的切线;
方法二:连接$OD$,$AD$,证$AD⊥BC$,$\because AB=AC$,$\therefore BD=CD$,$\because OA=OB$,$\therefore OD// AC$,……以下同方法一;
(2)连接$AD$,易证$BD=CD=2\sqrt {5}$,$\therefore AD=4\sqrt {5}$,
$\because AD\cdot CD=AC\cdot DE$,$\therefore DE=4$,
$\therefore OE=\sqrt {OD^{2}+DE^{2}}=\sqrt {41}$。
查看更多完整答案,请扫码查看


