1.图2是图1中拱形大桥的示意图,桥拱与桥面的交点为O,B,以点O为原点,水平直线OB为x轴,建立平面直角坐标系,桥拱可近似看成抛物线$y= -\frac {1}{400}(x-80)^{2}+16$,桥拱与桥墩AC的交点C恰好在水面,有$AC⊥x$轴,若$OA= 10$米,则桥面离水面的高度AC为(

A.$16\frac {9}{10}$米
B.$\frac {17}{4}$米
C.$16\frac {7}{40}$米
D.$\frac {15}{4}$米
B
)
A.$16\frac {9}{10}$米
B.$\frac {17}{4}$米
C.$16\frac {7}{40}$米
D.$\frac {15}{4}$米
答案:
B
2.一个足球被从地面向上踢出,它距地面的高度h(m)与足球被踢出后经过的时间t(s)之间具有函数关系$h= at^{2}+19.6t$,已知足球被踢出后经过4s落地,则足球距地面的最大高度是
19.6
m.
答案:
19.6
3.如图,要建一个圆形喷水池,在池中心竖直安装一根水管,在水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1米处达到最高,高度为3米,水柱落地处离池中心3米,水管长
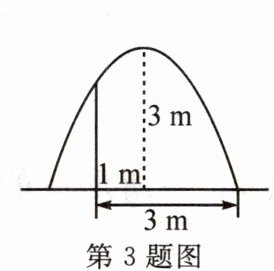
$\frac {9}{4}$
米.
答案:
$\frac {9}{4}$
4.如图,一桥拱呈抛物线状,桥的最大高度是16m,跨度是40m,在线段AB上离中心M处5m的地方,桥的高度是

15
m.
答案:
15
5.有一座抛物线形拱桥,正常水位时桥下面的AB宽20米,水位上升3米就达到警戒线CD,这时水面宽度为10米.
(1)在如图所示的坐标系中,求抛物线的表达式.
(2)若洪水到来时,再持续多少小时才能到拱桥顶(水位以每小时0.2米的速度上升)?
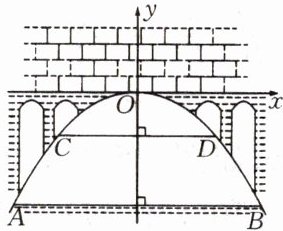
(1)在如图所示的坐标系中,求抛物线的表达式.
(2)若洪水到来时,再持续多少小时才能到拱桥顶(水位以每小时0.2米的速度上升)?

答案:
(1)$y=-\frac {1}{25}x^{2}$;
(2)再持续5小时到拱桥顶.
(1)$y=-\frac {1}{25}x^{2}$;
(2)再持续5小时到拱桥顶.
6.如图,某足球运动员站在点O处练习射门,将足球从离地面0.5m的A处正对球门踢出(点A在y轴上),足球的飞行高度y(单位:m)与飞行时间t(单位:s)之间满足函数关系式$y= at^{2}+5t+c$,已知足球飞行0.8s时,离地面的高度为3.5m.
(1)足球飞行的时间是多少时,足球离地面最高?最大高度是多少?
(2)若足球飞行的水平距离x(单位:m)与飞行时间t(单位:s)之间具有函数关系式$x= 10t$,已知球门的高度为2.44m,如果该运动员正对球门射门时,离球门的水平距离为28m,他能否将球直接射入球门?

(1)足球飞行的时间是多少时,足球离地面最高?最大高度是多少?
(2)若足球飞行的水平距离x(单位:m)与飞行时间t(单位:s)之间具有函数关系式$x= 10t$,已知球门的高度为2.44m,如果该运动员正对球门射门时,离球门的水平距离为28m,他能否将球直接射入球门?

答案:
(1)$y=-\frac {25}{16}t^{2}+5t+\frac {1}{2}=-\frac {25}{16}(t-\frac {8}{5})^{2}+\frac {9}{2}$,
当$t=\frac {8}{5}$时,$y_{最大}=\frac {9}{2}$;
(2)当$x=28$时,$t=2.8$.
当$t=2.8$时,$y=2.25<2.44$,
∴他能将球直接射入球门.
(1)$y=-\frac {25}{16}t^{2}+5t+\frac {1}{2}=-\frac {25}{16}(t-\frac {8}{5})^{2}+\frac {9}{2}$,
当$t=\frac {8}{5}$时,$y_{最大}=\frac {9}{2}$;
(2)当$x=28$时,$t=2.8$.
当$t=2.8$时,$y=2.25<2.44$,
∴他能将球直接射入球门.
查看更多完整答案,请扫码查看


