《2025年思维新观察九年级数学上册人教版》

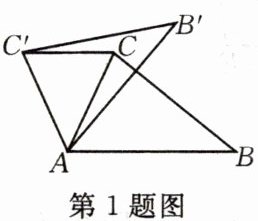
1.如图,在$\triangle ABC$中,$∠CAB= 65^{\circ }$,将$\triangle ABC$在平面内绕点A旋转到$\triangle AB'C'$的位置,使$CC'// AB$,则旋转角的度数为(C)

A.$35^{\circ }$
B.$40^{\circ }$
C.$50^{\circ }$
D.$65^{\circ }$

答案： C

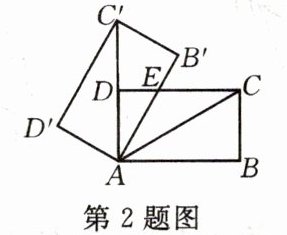
2.如图,将矩形ABCD绕点A旋转至矩形$AB'C'D'$的位置,此时$AC'$的中点恰好与D点重合,$AB'$交CD于点E.若$AB= 3$,则$\triangle AEC$的面积为(D)

A.3
B.1.5
C.$2\sqrt {3}$
D.$\sqrt {3}$

答案： D

3.如图,在$\triangle ABC$中,$∠A= 70^{\circ },AC= BC$,以点B为旋转中心把$\triangle ABC$按顺时针旋转α度,得到$\triangle A'BC'$,点$A'$恰好落在AC上,连接$CC'$,则$∠ACC'= $$110^{\circ}$.

答案： $110^{\circ}$

4.如图,正方形OABC绕着点O逆时针旋转$40^{\circ }$得到正方形ODEF,连接AF,则$∠OFA$的度数是(C)

A.$15^{\circ }$
B.$20^{\circ }$
C.$25^{\circ }$
D.$30^{\circ }$

答案： C

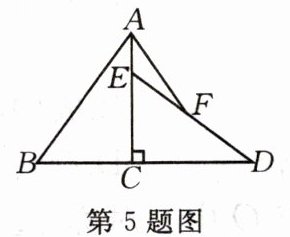
5.如图,已知$Rt\triangle ABC$中,$∠ACB= 90^{\circ },AC= 6,BC= 4$,将$\triangle ABC$绕直角顶点C顺时针旋转$90^{\circ }得到\triangle DEC$.若点F是DE的中点,连接AF,则$AF= $5.

答案： 5

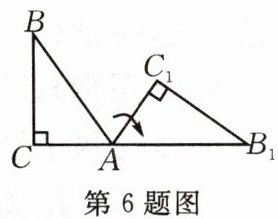
6.如图,将$Rt\triangle ABC$(其中$∠B= 35^{\circ },∠C= 90^{\circ }$)绕点A按顺时针方向旋转到$\triangle AB_{1}C_{1}$的位置,使得点$C,A,B_{1}$在同一条直线上,那么旋转角等于$125^{\circ}$.

答案： $125^{\circ}$

7.如图,正方形ABCD中,E为BC边上的一点,将$\triangle ABE旋转后得到\triangle CBF$.
(1)指出旋转中心及旋转的角度.
(2)判断AE与CF的数量和位置关系.
(3)如果正方形的面积是$18cm^{2},\triangle BCF的面积是5cm^{2}$,四边形AECD的面积是多少?

答案：
(1)旋转中心:点B,旋转角度为$90^{\circ}$;
(2)$AE=CF,AE⊥CF$;
(3)$S_{四边形AECD}=18-5=13(cm^{2})$.

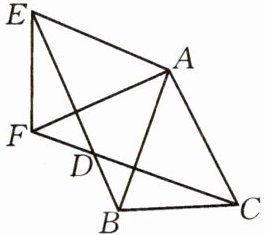
8.如图,$\triangle ABC$中,$AB= AC= 1,∠BAC= 45^{\circ },\triangle AEF是由\triangle ABC$绕点A按顺时针方向旋转得到的,连接BE,CF相交于点D.
(1)求证:$BE= CF;$
(2)当四边形ACDE为菱形时,求BD的长.

答案：
(1)$\because \triangle AEF$是由$\triangle ABC$绕点A按顺时针方向旋转得到的,$\therefore AE=AB,AF=AC,∠EAF=∠BAC$,
$\therefore ∠EAF+∠BAF=∠BAC+∠BAF$,即$∠EAB=$
$∠FAC$,
$\therefore \triangle AEB$可由$\triangle AFC$绕点A顺时针旋转得到,$\therefore BE=$CF;
(2)$\because$四边形ACDE为菱形,$AB=AC=1$,
$\therefore DE=AE=AC=AB=1,AC// DE$,
$\therefore ∠AEB=∠ABE=∠BAC=45^{\circ}$,
$\therefore \triangle ABE$为等腰直角三角形,$\therefore BE=\sqrt {2}$,
$\therefore BD=BE-DE=\sqrt {2}-1$.