1.如图,$\odot O$的半径为5,弦AB的长为8,点M是弦AB上的动点,则线段OM长的最小值为(

A.2
B.3
C.4
D.5
B
)
A.2
B.3
C.4
D.5
答案:
B
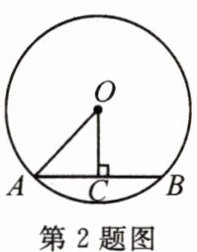
2.如图,在$\odot O$中,弦AB的长为4,圆心到弦AB的距离OC为2,则圆O的半径长是(
A.1
B.$\sqrt {2}$
C.$2\sqrt {2}$
D.4
C
)
A.1
B.$\sqrt {2}$
C.$2\sqrt {2}$
D.4
答案:
C
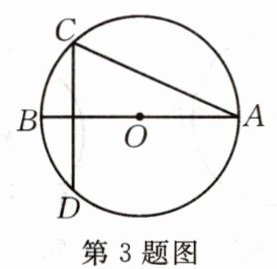
3.如图,$\odot O$的直径AB垂直于弦CD,$∠A= 22.5^{\circ },AB= 8$,则CD的长为(
A.$2\sqrt {2}$
B.4
C.$4\sqrt {2}$
D.8
C
)
A.$2\sqrt {2}$
B.4
C.$4\sqrt {2}$
D.8
答案:
C
4.如图,已知$\odot O的直径AB⊥CD$于点E,则下列结论中错误的是(

A.$CE= DE$
B.$AE= OE$
C.$\widehat {BC}= \widehat {BD}$
D.$△OCE\cong △ODE$
B
)
A.$CE= DE$
B.$AE= OE$
C.$\widehat {BC}= \widehat {BD}$
D.$△OCE\cong △ODE$
答案:
B
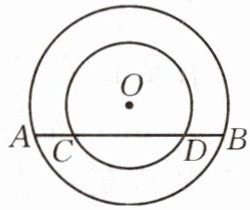
5.(教材P90习题9变式)如图,两个圆都以O为圆心,求证:$AD= BC$.

答案:
思路一:由证线段相等,联想证$\triangle OAC\cong \triangle OBD$.
思路二:由于弦CD,AB在一条直线上,可考虑过O作$OE\perp AB$于E,用垂径定理解决.
思路二:由于弦CD,AB在一条直线上,可考虑过O作$OE\perp AB$于E,用垂径定理解决.
6.如图,AD是$\odot O$的直径,BC是$\odot O$的弦,$AD⊥BC$,垂足为E,$AE= BC= 16$,求$\odot O$的直径.


答案:
连接OB,设$OB=OA=R$,则$OE=AE-AO=16-R$,
$\because OB^{2}=OE^{2}+BE^{2}$,$\therefore R^{2}=(16-R)^{2}+8^{2}$,解得$R=10$,
$\therefore \odot O$的直径为20.
$\because OB^{2}=OE^{2}+BE^{2}$,$\therefore R^{2}=(16-R)^{2}+8^{2}$,解得$R=10$,
$\therefore \odot O$的直径为20.
7.已知$\odot O的直径CD= 10$,弦$AB⊥CD$于M,且$AB= 8$,求弦AC的长.
答案:
$2\sqrt {5}$或$4\sqrt {5}$,$O,C$在弦$AB$两侧时,$AC=2\sqrt {5}$,$O,C$在弦$AB$同侧时,$AC=4\sqrt {5}$.
查看更多完整答案,请扫码查看


