1.如图,$□ ABCD$中,$\triangle AOB$绕着点

O
旋转$180^{\circ }$后,能够与△COD
重合,那么点A关于点O的对称点是C
,$\triangle AOD与\triangle COB$关于点O
成中心对称.
答案:
O △COD C O
2.如图,已知$\triangle ABC与\triangle ADE$关于点A成中心对称,若$AB= 2cm$,那么BD的长为____

4 cm
.
答案:
4 cm
3.下列四组图形中成中心对称的有(

A.1组
B.2组
C.3组
D.4组
C
)
A.1组
B.2组
C.3组
D.4组
答案:
C
4.下列说法正确的是(
A.全等的两个图形成中心对称
B.成中心对称的两个图形全等
C.成中心对称的两个图形必须重合
D.旋转后能够重合的两个图形成中心对称
B
)A.全等的两个图形成中心对称
B.成中心对称的两个图形全等
C.成中心对称的两个图形必须重合
D.旋转后能够重合的两个图形成中心对称
答案:
B
5.如图,已知$\triangle ABC与\triangle CDA$关于点O中心对称,过点O任作一直线EF分别交AD,BC于点E,F,下面的结论:①E和F,B和D是关于中心点O的对称点;②直线BD必经过点O;③四边形ABFO与四边形DEOC的面积必然相等;④$\triangle AOE与\triangle COF$成中心对称.其中正确的有(

A.1个
B.2个
C.3个
D.4个
D
)
A.1个
B.2个
C.3个
D.4个
答案:
D
6.如图,边长为2的正方形ABCD的对角线相交于点O,过点O的直线分别交边AD,BC于E,F两点,则阴影部分的面积是(
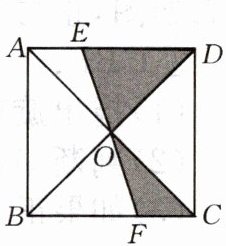
A.1
B.2
C.3
D.4
A
)
A.1
B.2
C.3
D.4
答案:
A
7.如图,在矩形ABCD中,点E在AD上,EC平分$∠BED$.
(1)求证:$\triangle BEC$为等腰三角形.
(2)在原图中画$\triangle FCE$,使它与$\triangle BEC$关于CE的中心点O成中心对称,此时四边形BCFE是什么图形?请说明理由.
(3)在(2)的条件下,若$DE= 2,CE= 2\sqrt {5}$,求BF的长.
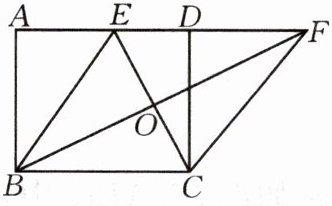
(1)求证:$\triangle BEC$为等腰三角形.
(2)在原图中画$\triangle FCE$,使它与$\triangle BEC$关于CE的中心点O成中心对称,此时四边形BCFE是什么图形?请说明理由.
(3)在(2)的条件下,若$DE= 2,CE= 2\sqrt {5}$,求BF的长.

答案:
(1)
∵AD//BC,
∴∠DEC=∠BCE,
∵∠DEC=∠BEC,
∴∠BEC=∠BCE,
∴△BCE是等腰三角形;
(2)
∵△FCE与△BEC关于CE的中点O成中心对称,
∴OB=OF,OE=OC,
∴四边形BCFE是平行四边形,
又
∵BC=BE,
∴四边形BCFE是菱形;
(3)易求CD=$\sqrt{CE^{2}-DE^{2}}$=4,设DF=x,则EF=x+2=CF,在△CDF中有:$x^{2}+4^{2}=(x+2)^{2}$,
∴x=3.
∴BO=$\sqrt{BE^{2}-OE^{2}}=\sqrt{5^{2}-(\sqrt{5})^{2}}=2\sqrt{5}$,BF=2BO=$4\sqrt{5}$.
(1)
∵AD//BC,
∴∠DEC=∠BCE,
∵∠DEC=∠BEC,
∴∠BEC=∠BCE,
∴△BCE是等腰三角形;
(2)
∵△FCE与△BEC关于CE的中点O成中心对称,
∴OB=OF,OE=OC,
∴四边形BCFE是平行四边形,
又
∵BC=BE,
∴四边形BCFE是菱形;
(3)易求CD=$\sqrt{CE^{2}-DE^{2}}$=4,设DF=x,则EF=x+2=CF,在△CDF中有:$x^{2}+4^{2}=(x+2)^{2}$,
∴x=3.
∴BO=$\sqrt{BE^{2}-OE^{2}}=\sqrt{5^{2}-(\sqrt{5})^{2}}=2\sqrt{5}$,BF=2BO=$4\sqrt{5}$.
查看更多完整答案,请扫码查看


