1.⊙O的半径为5cm,点A到圆心O的距离OA= 3cm,则点A与⊙O的位置关系为(
A.点A在⊙O上
B.点A在⊙O内
C.点A在⊙O外
D.无法确定
B
)A.点A在⊙O上
B.点A在⊙O内
C.点A在⊙O外
D.无法确定
答案:
B
2.在平面直角坐标系中,若⊙O是以原点为圆心,2为半径的圆,则点M(1,1)在(
A.⊙O内
B.⊙O外
C.⊙O上
D.不能确定
A
)A.⊙O内
B.⊙O外
C.⊙O上
D.不能确定
答案:
A
3.体育课上,小丽的铅球成绩为6.4m,假设小丽站在O处投铅球,如图,那么她投出的铅球落在(
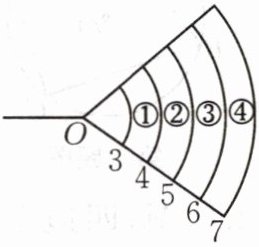
A.区域①
B.区域②
C.区域③
D.区域④
D
)
A.区域①
B.区域②
C.区域③
D.区域④
答案:
D
4.以点O为圆心,以3cm为半径作⊙O,若线段OP的长为8cm,那么OP的中点A与⊙O的位置关系是
点A在$\odot O$外
。
答案:
点A在$\odot O$外
5.已知点A在以O为圆心,3为半径的⊙O内,则点A到圆心O的距离d的范围是
$0\leqslant d<3$
。
答案:
$0\leqslant d<3$
6.已知⊙O的半径为1,点P到O的距离为R,且方程$x^{2}-2x+R= 0$有实数根,则点P(
A.在⊙O内
B.在⊙O上
C.在⊙O外
D.在⊙O内或⊙O上
D
)A.在⊙O内
B.在⊙O上
C.在⊙O外
D.在⊙O内或⊙O上
答案:
D
7.如图,在矩形ABCD中,AB= 4,AD= 3,以顶点D为圆心作半径为r的圆,若要求另外三个顶点A,B,C中至少有一个点在圆内,且至少有一个点在圆外,则r的取值范围是
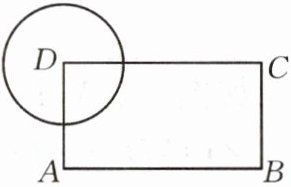
3<r<5
。
答案:
$3\lt r<5$
8.如图,在△ABC中,∠ACB= 90°,AC= 5cm,BC= 10cm,CD为中线,以点C为圆心,以$\frac{5}{2}\sqrt{5}$cm为半径作圆,试判断点A,B,D与⊙C的位置关系。
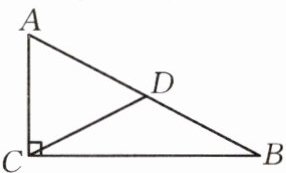

答案:
$\because AC=5cm$,$BC=10cm$$\therefore AB=5\sqrt{5}cm$,
$\therefore CD=\frac{1}{2}AB=\frac{5}{2}\sqrt{5}cm$,
$\because BC=10cm>\frac{5}{2}\sqrt{5}cm$,$\therefore$点B在$\odot C$的外部,
$\because AC=5cm<\frac{5}{2}\sqrt{5}cm$,$\therefore$点A在$\odot C$的内部,
$\because CD=\frac{5}{2}\sqrt{5}cm$,$\therefore$点D在$\odot C$上。
$\therefore CD=\frac{1}{2}AB=\frac{5}{2}\sqrt{5}cm$,
$\because BC=10cm>\frac{5}{2}\sqrt{5}cm$,$\therefore$点B在$\odot C$的外部,
$\because AC=5cm<\frac{5}{2}\sqrt{5}cm$,$\therefore$点A在$\odot C$的内部,
$\because CD=\frac{5}{2}\sqrt{5}cm$,$\therefore$点D在$\odot C$上。
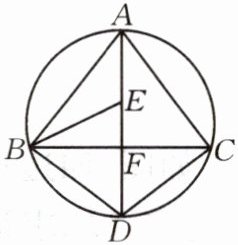
9.如图,AD为△ABC外接圆的直径,且AD⊥BC,垂足为点F,∠ABC的平分线交AD于点E,连接BD,CD。
(1)求证:BD= CD;
(2)请判断B,E,C三点是否在以D为圆心,DB长为半径的圆上,并说明理由。
(1)求证:BD= CD;
(2)请判断B,E,C三点是否在以D为圆心,DB长为半径的圆上,并说明理由。

答案:
(1)$\because AD$为圆的直径,$AD\perp BC$,$\therefore \overset{\frown }{BD}=\overset{\frown }{CD}$,$\therefore BD=CD$;
(2)B,E,C三点在以D为圆心,DB长为半径的圆上,理由:
$\because BE$平分$\angle ABC$,$\therefore \angle ABE=\angle EBF$,
$\because \angle BED=\angle BAD+\angle ABE$,$\angle EBD=\angle EBF+\angle CBD$,又$\because \angle CBD=\angle CAD=\angle BAD$,
$\therefore \angle BED=\angle EBD$,$\therefore DE=DB$,
又$\because DB=DC$,$\therefore DB=DE=DC$,
$\therefore$B,E,C三点在以D为圆心,DB长为半径的圆上。
(1)$\because AD$为圆的直径,$AD\perp BC$,$\therefore \overset{\frown }{BD}=\overset{\frown }{CD}$,$\therefore BD=CD$;
(2)B,E,C三点在以D为圆心,DB长为半径的圆上,理由:
$\because BE$平分$\angle ABC$,$\therefore \angle ABE=\angle EBF$,
$\because \angle BED=\angle BAD+\angle ABE$,$\angle EBD=\angle EBF+\angle CBD$,又$\because \angle CBD=\angle CAD=\angle BAD$,
$\therefore \angle BED=\angle EBD$,$\therefore DE=DB$,
又$\because DB=DC$,$\therefore DB=DE=DC$,
$\therefore$B,E,C三点在以D为圆心,DB长为半径的圆上。
10.如图,在△ABC中,∠ACB= 90°,AB= 10,BC= 8,CD⊥AB于点D,O为AB的中点。
(1)以点C为圆心,6为半径作圆C,试判断点A,D,B与⊙C的位置关系;
(2)①⊙C的半径为多少时,点O在⊙C上?
②⊙C的半径为多少时,点D在⊙C上?
(1)以点C为圆心,6为半径作圆C,试判断点A,D,B与⊙C的位置关系;
点A在圆上,B在圆外,点D在圆内
(2)①⊙C的半径为多少时,点O在⊙C上?
5
②⊙C的半径为多少时,点D在⊙C上?
4.8
答案:
(1)点A在圆上,B在圆外,点D在圆内;
(2)①$\odot C$的半径为5时,点O在$\odot C$上;
②$\odot C$的半径为4.8时,点D在$\odot C$上。
(1)点A在圆上,B在圆外,点D在圆内;
(2)①$\odot C$的半径为5时,点O在$\odot C$上;
②$\odot C$的半径为4.8时,点D在$\odot C$上。
查看更多完整答案,请扫码查看


