《2025年思维新观察九年级数学上册人教版》

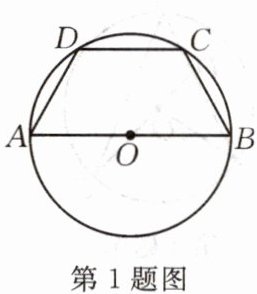
1.如图,已知$\odot O$的半径等于1cm,AB是直径,C,D是$\odot O$上的两点,且$\overset{\frown}{AD}= \overset{\frown}{DC}= \overset{\frown}{CB}$,则四边形ABCD的周长等于(B)

A.4cm
B.5cm
C.6cm
D.7cm

答案： B

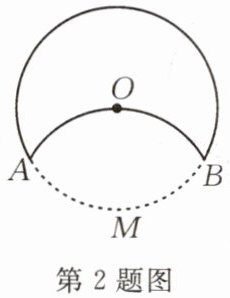
2.如图,将$\odot O$沿AB折叠后,圆弧恰好经过圆心,则$\overset{\frown}{AMB}$所对的圆心角等于(C)

A.$60^{\circ}$
B.$90^{\circ}$
C.$120^{\circ}$
D.$150^{\circ}$

答案： C

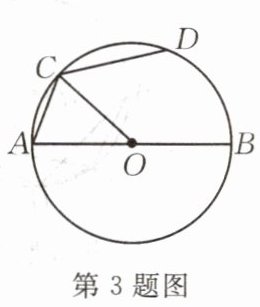
3.如图,AB是$\odot O$的直径,点C在$\odot O$上,$∠AOC= 40^{\circ}$,D是$\overset{\frown}{BC}$的中点,则$∠ACD= $125°。

答案： 125°

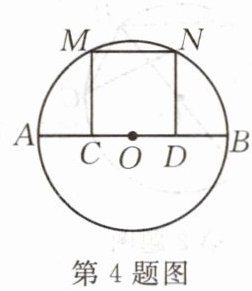
4.如图,在$\odot O$中,C、D分别是OA、OB的中点,$MC⊥AB$,$ND⊥AB$,M、N在$\odot O$上。下列结论：①$MC= ND$；②$\overset{\frown}{AM}= \overset{\frown}{MN}= \overset{\frown}{NB}$；③四边形MCDN是正方形；④$MN= \frac{1}{2}AB$。其中正确的结论是____①②④(填序号)。

答案： ①②④

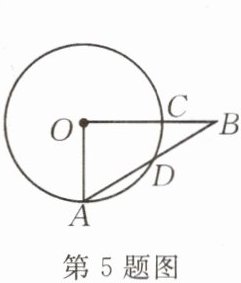
5.如图,在$\odot O$中,半径$OA⊥OC$,B是OC延长线上一点,AB与$\odot O$交于点D,$\overset{\frown}{AD}= 2\overset{\frown}{DC}$,则$∠B$的度数为30°。

答案： 30°

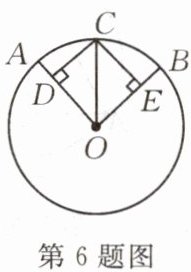
6.如图,D,E分别是$\odot O$的半径OA,OB上的点,$CD⊥OA$,$CE⊥OB$,$CD= CE$,则$\overset{\frown}{AC}与\overset{\frown}{CB}$的大小关系是$\overset{\frown}{AC}=\overset{\frown}{CB}$。

答案： $\overset{\frown}{AC}=\overset{\frown}{CB}$

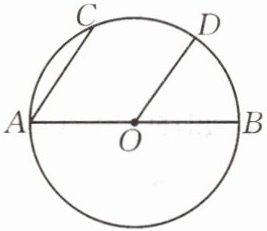
7.如图,AB是$\odot O$的直径,弦$AC// OD$。
(1)求证：$\overset{\frown}{BD}= \overset{\frown}{CD}$；
(2)若$\overset{\frown}{AC}所对圆心角的度数为58^{\circ}$,求$∠AOD$的度数。

答案：
(1)连接OC，
∵OA=OC，
∴∠OAC=∠ACO，
∵AC//OD，
∴∠BOD=∠OAC=∠ACO=∠COD，
∴$\overset{\frown}{BD}=\overset{\frown}{CD}$；
(2)
∵$\overset{\frown}{BD}=\overset{\frown}{CD}$，
∴∠COD=61°，
∴∠AOD=119°。

8.如图,半径为5的$\odot A$中,弦BC,ED所对的圆心角分别是$∠BAC$,$∠EAD$,若$DE= 6$,$∠BAC+∠EAD= 180^{\circ}$,求弦BC的长。

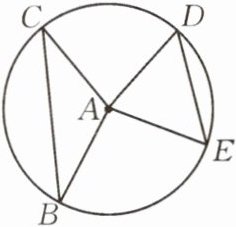
答案： 延长CA交⊙A于点F，连接BF，易证∠DAE=∠BAF，由AC=AB=AF及三角形内角和定理可证∠CBF=90°，在Rt△CBF中，由勾股定理可得BC=8。