《2025年名师学案八年级物理下册人教版》

7. 关于重心，下列说法正确的是（ ）
A. 空心的足球没有重心
B. 物体的重心不一定在物体上
C. 将质地均匀的木球的中心挖去后，木球的重心就消失了
D. 重心是物体上最重的一点

答案： 答案：B
解析：任何物体都有重心，空心的足球也有重心，A选项错误；物体的重心不一定在物体上，比如圆环的重心在其圆心处，不在圆环上，B选项正确；将质地均匀的木球的中心挖去后，木球的重心仍然存在，只是位置可能会发生变化，C选项错误；重心是物体各部分所受重力的等效作用点，不是物体上最重的一点，D选项错误。

8.（航天航空）2024年10月30日，我国成功发射神舟十九号载人航天飞船。若航天员在完全失重的太空轨道舱中进行体育锻炼，则下列活动中可采用的是（ ）
A. 拉力器
B. 举哑铃
C. 跳远
D. 吊环

答案： 答案：A
解析：在完全失重的太空轨道舱中，物体所受重力为零。举哑铃、跳远、吊环都需要依靠重力来完成，在失重状态下无法进行；而拉力器是通过拉伸弹簧来锻炼，与重力无关，在失重状态下可以使用，A选项正确。

9. 如图所示是一个抽奖的转盘，指针在正上方位置，若转盘的重心在A点，转动后它最终会停在（ ）
　　　　　　
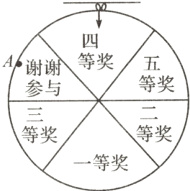
A. 一等奖
B. 二等奖
C. 三等奖
D. 谢谢参与

答案： 答案：B
解析：物体的重心越低越稳定，转盘转动后，重心A会处于最低位置，此时指针会指向二等奖区域，所以转盘最终会停在二等奖处，B选项正确。

10.（教材变式题）物体在月球表面受到的重力只有在地球表面的1/6，一个在地球上连同随身装备共重960 N的宇航员，质量为______ kg，在月球上的重力为______ N，质量为______ kg；一个举重运动员在地球上最多能举起150 kg的物体，到月球上他最多能举起________ kg的物体。（g = 10 N/kg）

答案： 答案：96 160 96 900 
解析：根据$G = mg$，可得宇航员在地球上的质量$m = G/g = 960$N÷10N/kg = 96kg，质量是物体的一种属性，不随位置的变化而变化，所以在月球上质量仍为96kg；在月球上的重力$G_{月}=\frac{1}{6}G_{地}=\frac{1}{6}×960$N = 160N；举重运动员在地球上能举起的物体重力$G = mg = 150$kg×10N/kg = 1500N，在月球上能举起的物体重力不变，仍为1500N，在月球上物体的重力$G_{月}=\frac{1}{6}G_{地}$，则在月球上能举起的物体质量$m_{月}=\frac{G_{月}}{g_{月}}=\frac{1500N}{\frac{1}{6}×10N/kg}=900$kg。

11.（科学探究）实验小组的同学测量出了不同质量钩码所受重力的多组数据，如下表:
　
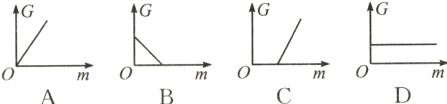
（1）根据实验测得的数据可知：物体所受重力G与物体质量m的比值为______ N/kg。
（2）分析表中数据，可以得出的结论是物体所受重力的大小与它的质量成________。
（3）根据表格中的数据可知，4个钩码所受重力大小为________ N。
（4）分析表中数据，下列图象中能正确表示物体所受重力与质量关系的是______。
　

答案： 答案：
(1)9.8　
(2)正比
(3)3.92　
(4)A
解析：（1）由表格数据可知，物体所受重力G与物体质量m的比值为$\frac{0.98N}{0.1kg}=\frac{1.96N}{0.2kg}=\frac{2.94N}{0.3kg}=9.8$N/kg；（2）因为物体所受重力G与物体质量m的比值是一个定值，所以物体所受重力的大小与它的质量成正比；（3）一个钩码质量为0.1kg，4个钩码质量为$m = 4×0.1$kg = 0.4kg，所受重力$G = mg = 0.4$kg×9.8N/kg = 3.92N；（4）物体所受重力与质量成正比，其图象是一条过原点的直线，A选项正确。

12.（教材改编题）一辆自重是5.0×10⁴ N的卡车，装载着25箱货物，每箱货物的质量是300 kg，行驶到一座立有限重标志（如图所示）的桥前。求：（g取10 N/kg）
（1）这辆车的总重力。
（2）要想安全过桥需要卸下几箱货物。
　　　　　　　　　　　　　　

答案： 答案：解：
(1)每箱货物的质量为$m_{1}=300$ kg，共有 25 箱货物，故车上所载货物的质量$m_{物}=25m_{1}=25×300$ kg = 7500 kg；因$g = 10$ N/kg，故货物的总重力$G_{物}=m_{物}g = 7500$ kg×10 N/kg = 7.5×10^{4} N；卡车自重$G_{车}=5.0×10^{4}$ N，这辆车的总重力$G_{总}=G_{车}+G_{物}=5.0×10^{4}$ N + 7.5×10^{4} N = 1.25×10^{5} N。
(2)汽车与货物的总质量$m_{总}=\frac{G_{总}}{g}=\frac{1.25×10^{5} N}{10 N/kg}=1.25×10^{4}$ kg = 12.5 t＞10 t，应卸下的货物质量$\Delta m = m_{总}-m_{限}=12.5$ t - 10 t = 2.5 t = 2500 kg，$n=\frac{\Delta m}{m_{1}}=\frac{2500 kg}{300 kg}\approx8.3$，因此要想安全过桥需要卸下 9 箱货物。
解析：（1）先根据每箱货物质量和箱数求出货物总质量，再根据$G = mg$求出货物总重力，最后将卡车自重和货物总重力相加得到车的总重力；（2）先根据$m = G/g$求出车和货物的总质量，与桥的限重比较，求出应卸下的货物质量，再用应卸下的货物质量除以每箱货物质量，得到需要卸下的箱数，由于箱数必须为整数，所以采用进一法取近似值。