《2025年全优少年课时训练六年级数学下册苏教版》

1. 选一选。
(1)做一个无盖的圆柱形铁皮水桶，所需的铁皮面积是(　　　　)。
(2)做一节圆柱形通风管道，所需的铁皮面积是(　　　　)。
(3)做一个圆柱形油桶，所需的铁皮面积是(　　　　)。
A. 侧面积
B. 侧面积 + 一个底面积
C. 侧面积 + 两个底面积

答案：
(1)B
(2)A
(3)C

2. 判一判。
(1)圆柱的底面半径扩大到原来的2倍，高不变，侧面积扩大到原来的4倍。(　　　　)
(2)圆柱的底面半径扩大到原来的2倍，高不变，表面积扩大到原来的4倍。(　　　　)
(3)圆柱的底面半径扩大到原来的2倍，高缩小为原来的$\frac{1}{2}$，表面积不变。 (　　　　)

答案：
(1)×
(2)×
(3)×

3. 填一填。
(1)一个圆柱形零件，它的底面直径是6分米，高是1.5米。这个圆柱形零件的表面积是(　　　　)平方分米。
(2)一根长为3米、底面直径为4分米的圆柱形木材，把它锯成同样长的5段，表面积比原来增加了(　　　　)平方分米。
(3)一个圆柱的高是10厘米，如果它的高减少3厘米，那么它的表面积比原来减少94.2平方厘米。原来圆柱的表面积是(　　　　)平方厘米。
(4)一个圆柱的底面直径是10厘米，高是4分米，它的侧面积是(　　　　)平方分米。
(5)李师傅要将一根铁皮通风管(如下图)平均锯成8段，管口直径为1.5米。每段铁皮的表面积是(　　　　)平方米。　　　

答案：
(1)339.12
(2)100.48
(3)471
(4)12.56
(5)11.775

4. (常考题)用铁皮做一个如右下图所示的通风管，需用铁皮多少平方厘米？

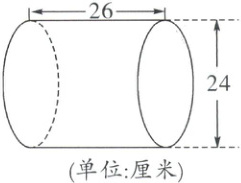
答案： $3.14×24×26 = 1959.36$(平方厘米)

5. (易错题)将一段高为1米的圆木沿直径劈成相等的两半，表面积增加了0.8平方米。原来圆木的表面积是多少平方米？
　　　　　　　

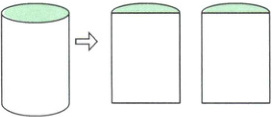
答案： $0.8÷2÷1 = 0.4$(米)
$3.14×(0.4÷2)^{2}×2 + 3.14×0.4×1 = 1.5072$(平方米)
[提示]增加的表面积即两个横截面(长方形)的面积，据此可以求出圆柱的底面直径。

6. 如右下图，卷筒纸的宽度是10厘米，中间硬纸轴的直径是4.2厘米。做一个中间硬纸轴，至少需要多少平方厘米的硬纸板？

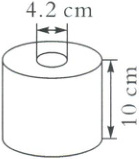
答案： $3.14×4.2×10 = 131.88$(平方厘米)
[提示]中间硬纸轴相当于一个无底面的圆柱，利用底面周长乘高可以求出侧面积，即需要的硬纸板面积。