《2025年全优少年课时训练六年级数学下册苏教版》

1. 填一填。
(1)一个圆锥的体积是16 dm³,与它等底等高的圆柱的体积是(　　)dm³。
(2)一个圆柱的底面半径是6 cm,高是7 cm,与它等底等高的圆锥的体积是(　　)cm³。
(3)把一个圆柱削成一个最大的圆锥,削去部分的体积是圆锥体积的(　　)倍,是圆柱体积的(　　)。
(4)一个底面直径是12厘米、高是10厘米的圆柱形钢坯能熔铸成(　　)个和它等底等高的圆锥,每个圆锥的体积是(　　)立方厘米。

答案：
(1)48 [提示]圆柱的体积是与它等底等高圆锥体积的3倍。
(2)263.76 [提示]圆锥的体积是与它等底等高圆柱体积的$\frac{1}{3}$。
(3)2 $\frac{2}{3}$ [提示]因为等底等高的圆柱和圆锥，圆锥的体积是圆柱体积的$\frac{1}{3}$，所以把一个圆柱削成一个最大的圆锥，圆锥的体积是圆柱体积的$\frac{1}{3}$，削去部分的体积是圆柱体积的$\frac{2}{3}$，削去部分的体积是圆锥体积的2倍。
(4)3 376.8 [提示]因为等底等高的圆柱和圆锥，圆柱的体积是圆锥的3倍，所以能熔铸成3个和它等底等高的圆锥，每个圆锥的体积是$\frac{1}{3}×3.14×(12÷2)^{2}×10 = 376.8$(立方厘米)。

2. 在建筑工地上,有一个近似于圆锥形的沙堆,测得底面直径是4米,高是1.5米。每立方米沙大约重1.7吨,这堆沙大约重多少吨?

答案： $\frac{1}{3}×3.14×(4÷2)^{2}×1.5 = 6.28$(立方米) 1.7×6.28 = 10.676(吨) [提示]先求出沙堆的体积，再求出这堆沙大约重多少吨。

3. 有一个底面半径是20 cm、高是15 cm的圆锥形的铁块,把它浸没在一个容积为30000 mL的盛满水的圆柱形桶中,水会溢出多少毫升?

答案： $\frac{1}{3}×3.14×20^{2}×15 = 6280(cm^{3})$ 6280 $cm^{3}$ = 6280 mL [提示]溢出水的体积等于铁块的体积。

4. 一个圆锥的底面周长是31.4 dm,高是120 cm,它的体积是多少立方分米?

答案： 31.4÷3.14÷2 = 5(dm) 120 cm = 12 dm $\frac{1}{3}×3.14×5^{2}×12 = 314(dm^{3})$ [提示]注意要换算成统一的单位。

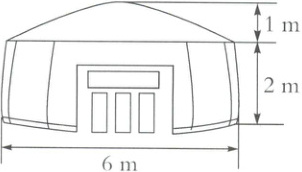
5. 下图的蒙古包是由圆柱和圆锥组成的,这个蒙古包所占的空间是多少立方米?
　　　　　

答案： $3.14×(6÷2)^{2}×2$ + $\frac{1}{3}×3.14×(6÷2)^{2}×1 = 65.94(m^{3})$ [提示]求这个蒙古包所占的空间是多少立方米，就是求底面直径为6 m、高为2 m的圆柱的体积与底面直径为6 m、高为1 m的圆锥的体积之和。

6. 将右下图的直角梯形ABCD,以DC为轴旋转一周,得到一个立体图形(上部分是圆锥,下部分是圆柱),它的体积是多少立方厘米?
　　　　　

答案： $12 - 9 = 3(cm)$
$3.14×4^{2}×9$ + $\frac{1}{3}×3.14×4^{2}×3 = 502.4(cm^{3})$
[提示]立体图形的体积可分为两部分，上部分是底面半径为4 cm、高为12 - 9 = 3(cm)的圆锥；下部分是底面半径为4 cm、高为9 cm的圆柱，分别算出它们的体积再相加即可。

7. 一个圆锥形木块,沿底面直径分成形状、大小都相同的两半,表面积比原来增加了48 cm²。已知木块的高是5 cm,则木块的体积是多少立方厘米?

答案： 48÷2×2÷5 = 9.6(cm) $\frac{1}{3}×3.14×(9.6÷2)^{2}×5 = 120.576(cm^{3})$ [提示]将圆锥沿底面直径分成形状、大小都相同的两半，截面是三角形，表面积比原来增加了2个相同三角形的面积，先算出三角形的底，也就是圆锥的底面直径，再求出木块的体积。

8. 一个长方体容器,从里面量,长15 cm,宽12 cm。容器内装有10 cm深的水,放入一个底面半径为5 cm的圆锥形金属零件使其全部浸入水中,水面升高到11.57 cm(水未溢出)。这个圆锥形零件的高是多少?

答案： $15×12×(11.57 - 10) = 282.6(cm^{3})$ $282.6×3÷(3.14×5^{2}) = 10.8(cm)$ [提示]圆锥形金属零件的体积就等于长方体容器中水面升高部分的体积，先求出圆锥形金属零件的体积，再根据底面半径和体积求出圆锥的高。