《2025年全优少年课时训练六年级数学下册苏教版》

1. 王叔叔将一个高是6分米的圆柱形木材切成3段小圆柱，表面积增加了12平方分米。原来圆柱形木材的体积是多少立方分米？

答案： $12\div[(3 - 1)\times2]=3$（平方分米）
$3\times6 = 18$（立方分米）
[提示]圆柱沿着底面切开，切成3段要切2次，切一次多出2个底面，增加的表面积等于$(3 - 1)\times2 = 4$（个）底面积之和。

2. 将一个圆柱的侧面沿高展开，得到一个边长是25.12厘米的正方形。这个圆柱的底面积是多少平方厘米？

答案： $25.12\div3.14\div2 = 4$（厘米）
$3.14\times4^{2}=50.24$（平方厘米）
[提示]由圆柱侧面展开图的特点可知：这个圆柱的底面周长等于正方形的边长。先求出圆柱的底面半径，再求出圆柱的底面积。

3. 将一个高是9分米、底面半径是2分米的圆柱形铁块，重新锻造成一个高是9分米的圆锥。圆锥的底面积是多少平方分米？

答案： $3.14\times2^{2}\times3 = 37.68$（平方分米）
[提示]体积相等、高也相等的圆柱形铁块和圆锥形铁块，圆锥形铁块的底面积是圆柱形铁块底面积的3倍。

4. 下图是一个圆柱形水桶，把一根半径是5厘米的圆柱形铁块全部浸入水中，水面上升9厘米；把铁块竖着提出水面8厘米后，水面下降4厘米。求圆柱形铁块的体积。（铁块上的水忽略不计）

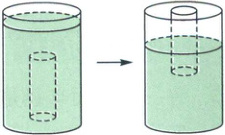
答案： 提出水面部分的圆柱形铁块体积：$3.14\times5^{2}\times8 = 628$（立方厘米）
水桶的底面积：$628\div4 = 157$（平方厘米）
圆柱形铁块的体积：$157\times9 = 1413$（立方厘米）
[提示]因为圆柱形铁块全部浸入水中，所以“水面上升9厘米”这部分水的体积与圆柱形铁块的体积相等；“水面下降4厘米”这部分水的体积与8厘米长的圆柱形铁块的体积相等。根据8厘米长的圆柱形铁块的体积，就可以计算出圆柱形水桶的底面积，从而求出圆柱形铁块的体积。

5. 单板滑雪U型池赛是冬奥会的比赛项目，比赛在一个形状类似于U型的槽子里进行，结构由宽阔平坦的底部和两侧的四分之一的圆管组成（模型图和截面图如下）。请计算下面U型池面的面积。

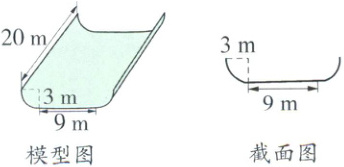
答案： $3.14\times3\times2\times20\times\frac{1}{2}+20\times9 = 368.4$（$m^{2}$）
[提示]U型池面的面积 = 圆柱侧面积的一半 + 底面长方形的面积