2025年金版新学案高中物理选择性必修第三册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年金版新学案高中物理选择性必修第三册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第8页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
例 1 在用油膜法估测油酸分子的大小的实验中,小娜和小问同学组成的小组具体操作如下:
①取纯油酸 0.1 mL 注入 500 mL 的容量瓶内,然后向瓶中加入酒精,直到液面达到 500 mL 的刻度为止,摇动容量瓶使油酸在酒精中充分溶解,形成油酸酒精溶液;
②用滴管吸取制得的溶液逐滴滴入量筒,记录滴入的滴数直到量筒达到 1.0 mL 为止,共滴了 25 滴;
③在边长约 30 cm 的浅盘内注入约 2 cm 深的水,将爽身粉均匀地撒在水面上,再用滴管吸取油酸酒精溶液,轻轻地向水面滴一滴油酸酒精溶液,油酸在水面上尽可能地散开,形成一层油膜,可以清楚地看出油膜轮廓;
④待油膜形状稳定后,将事先准备好的玻璃板放在浅盘上,并在玻璃板上描下油膜的轮廓;
⑤将画有油膜轮廓的玻璃板放在坐标纸上,如图 1 所示,可以数出轮廓范围内小方格的个数,小方格的边长为 $L = 1 cm$。
(1) 根据该小组的实验数据,可估算出油酸分子的直径约为
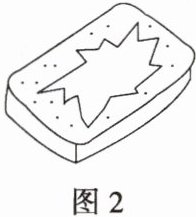
(2) 某次实验时,小娜同学滴下油酸酒精溶液后,爽身粉迅速散开形成如图 2 所示的“锯齿”边缘图案,导致油膜没有充分展开。
①出现该图样的原因可能是
A. 盆中装的水量太多
B. 爽身粉撒得太多,且厚度不均匀
C. 盆太小导致油酸无法形成单分子层
②若用此油膜作为依据进行估测,则最终的测量结果将
(3) 实验中总会有各种意外,小问同学作为物理课代表,就在实验时细心地发现三位同学各发生了一个操作失误,其中导致最后所测分子直径偏大的是
A. 甲同学在配制油酸酒精溶液时,不小心把酒精倒多了一点
B. 乙同学在计算注射器滴出的每一滴油酸酒精溶液体积后,不小心拿错了一个注射器取一滴油酸酒精溶液滴在水面上,这个拿错的注射器的针管比原来的粗
C. 丙同学计算油膜面积时,把所有半格左右的油膜都算成了一格

①取纯油酸 0.1 mL 注入 500 mL 的容量瓶内,然后向瓶中加入酒精,直到液面达到 500 mL 的刻度为止,摇动容量瓶使油酸在酒精中充分溶解,形成油酸酒精溶液;
②用滴管吸取制得的溶液逐滴滴入量筒,记录滴入的滴数直到量筒达到 1.0 mL 为止,共滴了 25 滴;
③在边长约 30 cm 的浅盘内注入约 2 cm 深的水,将爽身粉均匀地撒在水面上,再用滴管吸取油酸酒精溶液,轻轻地向水面滴一滴油酸酒精溶液,油酸在水面上尽可能地散开,形成一层油膜,可以清楚地看出油膜轮廓;
④待油膜形状稳定后,将事先准备好的玻璃板放在浅盘上,并在玻璃板上描下油膜的轮廓;
⑤将画有油膜轮廓的玻璃板放在坐标纸上,如图 1 所示,可以数出轮廓范围内小方格的个数,小方格的边长为 $L = 1 cm$。
(1) 根据该小组的实验数据,可估算出油酸分子的直径约为
$7 × 10^{-10}$
m(结果保留 1 位有效数字)。(2) 某次实验时,小娜同学滴下油酸酒精溶液后,爽身粉迅速散开形成如图 2 所示的“锯齿”边缘图案,导致油膜没有充分展开。
①出现该图样的原因可能是
B
。A. 盆中装的水量太多
B. 爽身粉撒得太多,且厚度不均匀
C. 盆太小导致油酸无法形成单分子层
②若用此油膜作为依据进行估测,则最终的测量结果将
偏大
(选填“偏大”“偏小”或“无影响”),经过评估,该小组决定重做实验。(3) 实验中总会有各种意外,小问同学作为物理课代表,就在实验时细心地发现三位同学各发生了一个操作失误,其中导致最后所测分子直径偏大的是
A
。A. 甲同学在配制油酸酒精溶液时,不小心把酒精倒多了一点
B. 乙同学在计算注射器滴出的每一滴油酸酒精溶液体积后,不小心拿错了一个注射器取一滴油酸酒精溶液滴在水面上,这个拿错的注射器的针管比原来的粗
C. 丙同学计算油膜面积时,把所有半格左右的油膜都算成了一格


答案:
(1)$7 × 10^{-10}$
(2)①B ②偏大
(3)A
解析:
(1)依题意,一滴溶液中纯油酸的体积为$V = \frac{0.1}{500} × \frac{1}{25} mL = 8 × 10^{-12} m^{3}$,单分子油膜的面积为$S = 116 × 1 × 10^{-4} m^{2} = 1.16 × 10^{-2} m^{2}$,则油酸分子的直径为$d = \frac{V}{S} \approx 7 × 10^{-10} m$。
(2)①出现该图样的原因可能是爽身粉撒得太多,且厚度不均匀。故选B。
②依题意,油膜没有充分展开,对应的油膜面积偏小,根据$d = \frac{V}{S}$,可知最终的测量结果将偏大。
(3)甲同学不小心把酒精倒多了一点,会导致油酸浓度比计算值小了一些,算出的一滴油酸酒精溶液中纯油酸的体积比实际值大,由$d = \frac{V}{S}$可知最后所测的分子直径偏大,故A正确;乙同学拿错的注射器的针管比原来的粗,一滴油酸酒精溶液的实际体积变大,一滴油酸酒精溶液中纯油酸的体积变大,对应的油膜面积S变大,但体积V还是按原来细的算,由$d = \frac{V}{S}$可知最后所测的分子直径偏小,故B错误;丙同学把所有半格左右的油膜都算成了一格,计算出的油膜的面积S偏大,由$d = \frac{V}{S}$可知最后所测的分子直径偏小,故C错误。
(1)$7 × 10^{-10}$
(2)①B ②偏大
(3)A
解析:
(1)依题意,一滴溶液中纯油酸的体积为$V = \frac{0.1}{500} × \frac{1}{25} mL = 8 × 10^{-12} m^{3}$,单分子油膜的面积为$S = 116 × 1 × 10^{-4} m^{2} = 1.16 × 10^{-2} m^{2}$,则油酸分子的直径为$d = \frac{V}{S} \approx 7 × 10^{-10} m$。
(2)①出现该图样的原因可能是爽身粉撒得太多,且厚度不均匀。故选B。
②依题意,油膜没有充分展开,对应的油膜面积偏小,根据$d = \frac{V}{S}$,可知最终的测量结果将偏大。
(3)甲同学不小心把酒精倒多了一点,会导致油酸浓度比计算值小了一些,算出的一滴油酸酒精溶液中纯油酸的体积比实际值大,由$d = \frac{V}{S}$可知最后所测的分子直径偏大,故A正确;乙同学拿错的注射器的针管比原来的粗,一滴油酸酒精溶液的实际体积变大,一滴油酸酒精溶液中纯油酸的体积变大,对应的油膜面积S变大,但体积V还是按原来细的算,由$d = \frac{V}{S}$可知最后所测的分子直径偏小,故B错误;丙同学把所有半格左右的油膜都算成了一格,计算出的油膜的面积S偏大,由$d = \frac{V}{S}$可知最后所测的分子直径偏小,故C错误。
例 2(2025·河北唐山高二统考)在“用油膜法估测油酸分子的大小”的实验中,油酸酒精溶液的浓度为每 1 000 mL 油酸酒精溶液中有油酸 0.5 mL,用滴管向量筒内滴 100 滴上述溶液,量筒中的溶液体积增加 1 mL。若把一滴这样的溶液滴入盛水的浅盘中,由于酒精溶于水,油酸在水面展开,稳定后形成单分子油膜的形状如图所示。(以下计算结果均保留 1 位有效数字)
(1) 若每一小方格的边长为 10 mm,则油膜的面积为
(2) 每滴油酸酒精溶液中含有纯油酸的体积为
(3) 根据上述数据,估算出油酸分子的直径为
(4) 为了尽可能准确地估测出油酸分子的大小,下列措施可行的是
A. 油酸浓度适当大一些
B. 油酸浓度适当小一些
C. 油酸扩散后立即绘出轮廓图
D. 油酸扩散后收缩,待其稳定后再绘出轮廓图

(1) 若每一小方格的边长为 10 mm,则油膜的面积为
$8 × 10^{-3}$
$m^2$。(2) 每滴油酸酒精溶液中含有纯油酸的体积为
$5 × 10^{-12}$
$m^3$。(3) 根据上述数据,估算出油酸分子的直径为
$6 × 10^{-10}$
m。(4) 为了尽可能准确地估测出油酸分子的大小,下列措施可行的是
BD
。A. 油酸浓度适当大一些
B. 油酸浓度适当小一些
C. 油酸扩散后立即绘出轮廓图
D. 油酸扩散后收缩,待其稳定后再绘出轮廓图
答案:
(1)$8 × 10^{-3}$
(2)$5 × 10^{-12}$
(3)$6 × 10^{-10}$
(4)BD
解析:
(1)每个正方形的面积为$S_{1} = (10^{-2})^{2} m^{2} = 1 × 10^{-4} m^{2}$,面积超过正方形面积一半的正方形的个数为81,则油膜的面积为$S = 81S_{1} = 81 × 10^{-4} m^{2} \approx 8 × 10^{-3} m^{2}$。
(2)每滴油酸酒精溶液中含有纯油酸的体积$V = \frac{0.5}{1000} × \frac{1}{100} mL = 5 × 10^{-12} m^{3}$。
(3)把油酸分子看成球形,且不考虑分子间的空隙,则分子的直径为$d = \frac{V}{S} = \frac{5 × 10^{-12}}{8 × 10^{-3}} m \approx 6 × 10^{-10} m$。
(4)为能形成单分子油膜,油酸浓度应适当小些;油酸扩散后收缩,绘制轮廓图应在其稳定后进行。故选BD。
(1)$8 × 10^{-3}$
(2)$5 × 10^{-12}$
(3)$6 × 10^{-10}$
(4)BD
解析:
(1)每个正方形的面积为$S_{1} = (10^{-2})^{2} m^{2} = 1 × 10^{-4} m^{2}$,面积超过正方形面积一半的正方形的个数为81,则油膜的面积为$S = 81S_{1} = 81 × 10^{-4} m^{2} \approx 8 × 10^{-3} m^{2}$。
(2)每滴油酸酒精溶液中含有纯油酸的体积$V = \frac{0.5}{1000} × \frac{1}{100} mL = 5 × 10^{-12} m^{3}$。
(3)把油酸分子看成球形,且不考虑分子间的空隙,则分子的直径为$d = \frac{V}{S} = \frac{5 × 10^{-12}}{8 × 10^{-3}} m \approx 6 × 10^{-10} m$。
(4)为能形成单分子油膜,油酸浓度应适当小些;油酸扩散后收缩,绘制轮廓图应在其稳定后进行。故选BD。
查看更多完整答案,请扫码查看


