《2025年新课程新教材导航学七年级数学上册北师大版》

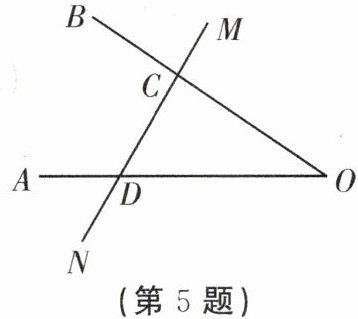
5. 如图，在 $ OB $ 边上取一点 $ C $，过点 $ C $ 作直线 $ MN $ 交 $ OA $ 于点 $ D $，图中所有角(平角除外)有9个，其中 $ \angle BCN $ 和∠BCM或∠DCO构成平角。

答案： 5.9 ∠BCM或∠DCO

6. 爱钻研的亮亮发现将图 1 所示的手表，理解成图 2 的数学模型(点 $ A $ 和点 $ D $ 是表带的两端，点 $ A $，$ B $，$ C $，$ D $ 在同一条线段上)，可以产生下面的数学问题。
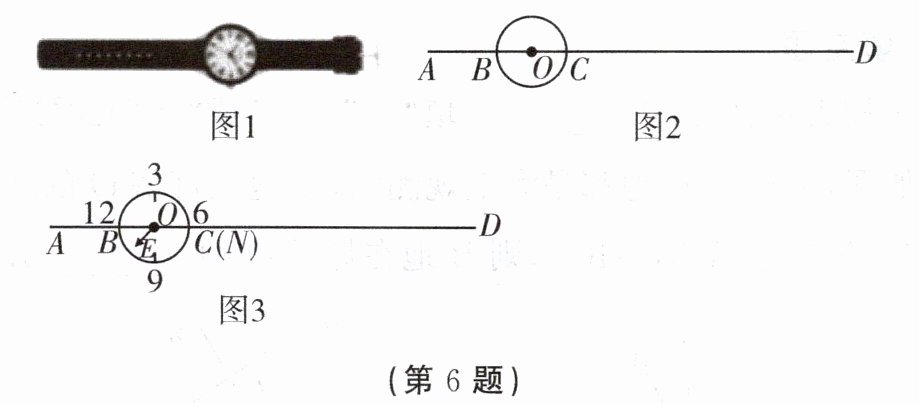
(1)已知表盘直径 $ BC $ 为 $ 4 cm $，$ CD = 4AB $，若点 $ B $ 是 $ AC $ 的中点，则表带 $ CD = $16 $ cm $。
(2)在某个时刻，分针 $ ON $ 指向表盘上的数字“6”(此时 $ ON $ 与 $ OC $ 重合)。时针为 $ OE $，表盘显示时间为 $ 10:30 $，如图 3 所示。
① $ 10:30 $ 时分针和时针的夹角为135 $ ^{\circ} $。
②作射线 $ OF $，使 $ \angle EOF = 20^{\circ} $，求此时 $ \angle BOF $ 的度数。

答案： 6.
(1)16
(2) ①135 ②解：由①知，∠EOC = 135°，所以∠BOE = 180° - 135° = 45°.当OF在∠EOB内部时，∠BOF = ∠BOE - ∠EOF = 25°；当OF在∠EOB外部时，∠BOF = ∠BOE + ∠EOF = 65°. 综上所述，∠BOF的度数为25°或65°.