《2025年全程检测单元测试卷八年级数学上册沪教版》

18. (12分)在同一平面直角坐标系中,正比例函数 $ y = 2x $ 与一次函数 $ y = - x + m $($ m $ 为常数)的图象交于点 $ M(1,k) $.
(1)(6分)求一次函数的表达式.
(2)(6分)求一次函数图象与两坐标轴围成的三角形的面积.

答案： 18.
(1)因为点$M(1,k)$在函数$y = 2x$的图象上，所以$k = 2$.所以点$M$的坐标为$(1,2)$.又因为点$M$也在一次函数$y=-x+m$的图象上，所以$2=-1+m$，解得$m = 3$.所以一次函数的表达式为$y=-x+3$.
(2)在一次函数$y=-x+3$中，令$x = 0$，得$y = 3$；令$y = 0$，得$x = 3$.所以函数图象与两坐标轴的交点分别为$(0,3)$，$(3,0)$，所围成的三角形的面积为$\frac{1}{2} × 3 × 3=\frac{9}{2}$.

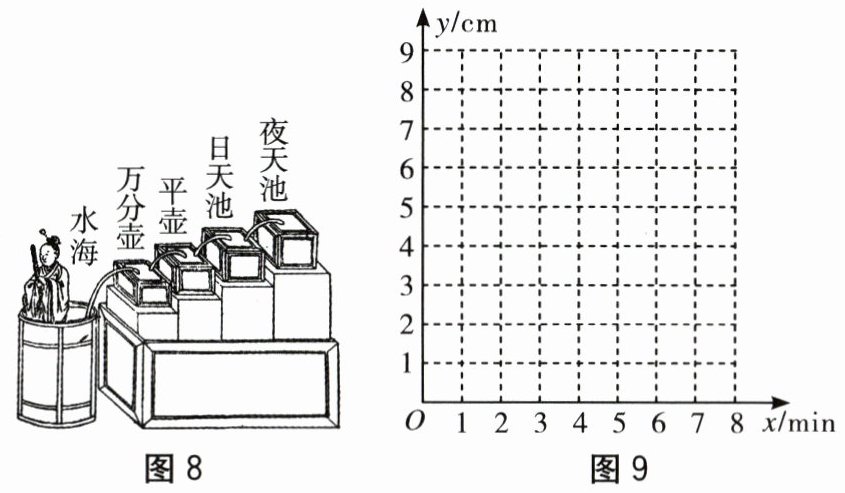
19. (14分)【问题情境】漏刻是我国古代的一种计时工具,据史书记载,西周时期已经出现了漏刻,这是我国古代人民对函数思想的应用.如图8,数学兴趣小组根据漏刻的原理制作了一个简单的漏刻计时工具模型,并从函数的角度进行了实验探究.兴趣小组每分钟记录一次水位的读数,得到下表:

【探索发现】
(1)(4分)建立平面直角坐标系,如图9所示,横轴表示供水时间 $ x $,纵轴表示水位读数 $ y $,请你在平面直角坐标系中描出以上表中的数据为坐标的各点.
(2)(4分)将各点连线,并观察这些点是否在同一直线上.如果在同一直线上,请你建立适当的函数模型,并求出函数表达式;如果不在,请说明理由.
(3)(3分)若供水时间为10min,水位读数是多少?
(4)(3分)若这次实验从9:00开始第一次计时时,求当水位读数是15cm时的时间.

答案：
19.
(1)如图5所示.

(2)如图6所示，这些点在同一直线上.设直线对应的函数表达式为$y=kx+b$.把点$(0,5)$，$(2,6)$代入，得$\begin{cases}b = 5,\\2k + b = 6.\end{cases}$解得$\begin{cases}k = 0.5,\\b = 5.\end{cases}$所求函数表达式为$y=0.5x+5$.
(3)当$x = 10$时，$y=0.5 × 10+5=10$.若供水时间为$10min$时，则水位读数是$10cm$.
(4)当$y = 15$时，$0.5x+5=15$.解得$x = 20$，即供水时间为$20min$.因为这次实验从$9:00$开始第一次计时，所以水位读数是$15cm$时是$9:20$.