2025年全程检测单元测试卷八年级数学上册沪教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年全程检测单元测试卷八年级数学上册沪教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
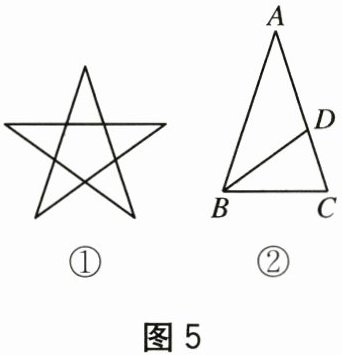
8. 锐角黄金三角形是顶角为 $36^{\circ}$ 的等腰三角形,其底边与腰长的比为黄金比例,在五角星(如图 5①)中含有 5 个锐角黄金三角形。如图 5②,在 $\triangle ABC$ 中,$AB = AC$,$\angle A = 36^{\circ}$,$BD$ 平分 $\angle ABC$,交 $AC$ 于点 $D$,则 $\angle CDB$ 的度数是(
A.$36^{\circ}$
B.$70^{\circ}$
C.$72^{\circ}$
D.$80^{\circ}$
A
)。
A.$36^{\circ}$
B.$70^{\circ}$
C.$72^{\circ}$
D.$80^{\circ}$


答案:
8.A [解析]
∵AB=AC=4,
∴∠B=∠C.
∵∠1=∠C,
∴∠B=∠1.又
∵∠ADB+∠EDC=180°−∠1,∠BAD+∠ADB=180°−∠B.
∴∠BAD=∠EDC.
∵AD=DE,
∴△ABD≌△DCE(AAS).
∴AB=CD=4,BD=CE.
∵BC=6,
∴CE=BD=BC−CD=6−4=2.
∴AE=AC−CE=4−2=2.故选A.
∵AB=AC=4,
∴∠B=∠C.
∵∠1=∠C,
∴∠B=∠1.又
∵∠ADB+∠EDC=180°−∠1,∠BAD+∠ADB=180°−∠B.
∴∠BAD=∠EDC.
∵AD=DE,
∴△ABD≌△DCE(AAS).
∴AB=CD=4,BD=CE.
∵BC=6,
∴CE=BD=BC−CD=6−4=2.
∴AE=AC−CE=4−2=2.故选A.
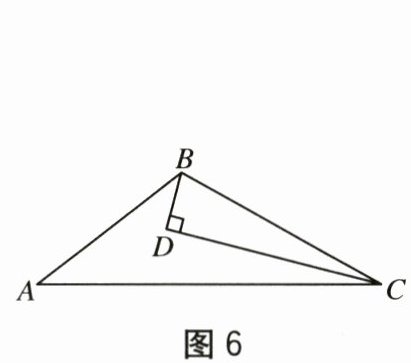
9. 如图 6,$D$ 为 $\triangle ABC$ 内一点,$CD$ 平分 $\angle ACB$,$BD\perp CD$,垂足为 $D$,$\angle ABD = \angle A$。若 $BD = 1$,$BC = 4$,则 $AC$ 的长为(
A.6
B.3
C.4
D.5
D
)。A.6
B.3
C.4
D.5
答案:
9.D[解析]由∠CAE=∠BAD可得∠CAB=∠DAE.又由AC=AD,①添加条件AB=AE,结合上述条件,可用“SAS”判定△ABC≌△AED;②添加条件BC=ED,结合上述条件,无法判定△ABC≌△ADE;③添加条件∠C=∠D,结合上述条件,可用“ASA”判定△ABC≌△AED;④添加条件∠B=∠E,结合上述条件,可用“AAS”判定△ABC≌△AED.故选D.
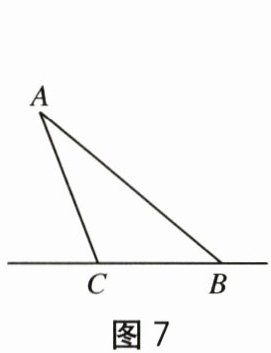
10. 如图 7,在 $\triangle ABC$ 中,$\angle ABC = 40^{\circ}$,动点 $D$ 在直线 $BC$ 上。当 $\triangle ABD$ 为等腰三角形时,点 $D$ 的位置可能情况有(
A.1 种
B.2 种
C.3 种
D.4 种
D
)。A.1 种
B.2 种
C.3 种
D.4 种
答案:
10.D[解析]在△ABC中,AB−AC<BC<AB+AC,即10−7<BC<10+7,3<BC<17.如图16,延长AD至点E,使DE=AD,连接BE.
∵AD是△ABC的边BC上的中线,
∴BD=CD.又
∵∠BDE=∠ADC,DE=AD,
∴△EBD≌△ACD(SAS).
∴BE=AC=7.在△ABE中,AB−BE<AE<AB+BE,即AB−AC<AE<AB+AC,即10−7<AE<10+7,即3<AE<17.
∴1.5<AD<8.5.故选D.

10.D[解析]在△ABC中,AB−AC<BC<AB+AC,即10−7<BC<10+7,3<BC<17.如图16,延长AD至点E,使DE=AD,连接BE.
∵AD是△ABC的边BC上的中线,
∴BD=CD.又
∵∠BDE=∠ADC,DE=AD,
∴△EBD≌△ACD(SAS).
∴BE=AC=7.在△ABE中,AB−BE<AE<AB+BE,即AB−AC<AE<AB+AC,即10−7<AE<10+7,即3<AE<17.
∴1.5<AD<8.5.故选D.

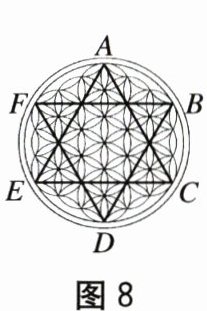
11. “生命之花”是一种古老的几何图案,由多个等圆相交构成,象征生命与宇宙的和谐。现简化其基础图形如图 8 所示,将圆六等分(等分点分别记为 $A$,$B$,$C$,$D$,$E$,$F$),每隔一个点连接成线段(如 $A\to C\to E\to A$,$B\to D\to F\to B$),形成六芒星状图案。该图形共有
AB=DC(或OA=OD或OB=OC)
条对称轴,图中所有小三角形均为三角形,相邻两条线段(如 $AC$ 与 $CE$)的夹角为。


答案:
11.AB=DC(或OA=OD或OB=OC) [解析]由AB//CD可得∠A=∠D,∠B=∠C.由图形可知∠AOB=∠DOC,故需添加对应边相等的条件,用“ASA”或“AAS”来判定全等.
12. 在 $Rt\triangle ABC$ 中,$\angle C = 90^{\circ}$,$AD$ 平分 $\angle BAC$ 交 $BC$ 于点 $D$。若 $CD = 4$,则点 $D$ 到 $AB$ 的距离是
HL
。
答案:
12.HL [解析]
∵OM⊥MP,ON⊥NP,
∴∠OMP=∠ONP=90°.在Rt△POM和Rt△PON中,OP=OP,PM=PN,因此可用“HL”判定两个三角形全等.
∵OM⊥MP,ON⊥NP,
∴∠OMP=∠ONP=90°.在Rt△POM和Rt△PON中,OP=OP,PM=PN,因此可用“HL”判定两个三角形全等.
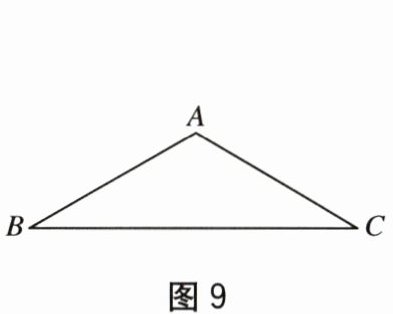
13. 在某次大数据产业博览会上,“自动化立体库”中有许多几何元素,其中有一个等腰三角形模型(示意图如图 9 所示),它的顶角为 $120^{\circ}$,腰长为 $12$ m,则底边上的高是
2
。
答案:
13.2 [解析]
∵∠ABC=90°,AD⊥BD,CE⊥BD,
∴∠D=∠CEB=∠ABC=90°.
∴∠ABD+∠CBE=90°,∠ABD+∠BAD=90°.
∴∠CBE=∠BAD.
∵AB=BC,
∴△ABD≌△BCE (AAS).
∴BD=CE=5,AD=BE=3.
∴DE=BD−BE=5−3=2.
∵∠ABC=90°,AD⊥BD,CE⊥BD,
∴∠D=∠CEB=∠ABC=90°.
∴∠ABD+∠CBE=90°,∠ABD+∠BAD=90°.
∴∠CBE=∠BAD.
∵AB=BC,
∴△ABD≌△BCE (AAS).
∴BD=CE=5,AD=BE=3.
∴DE=BD−BE=5−3=2.
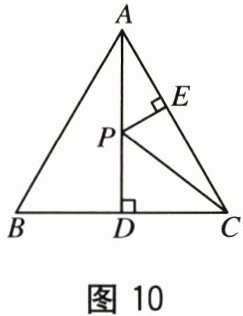
14. 如图 10,在 $\triangle ABC$ 中,$AB = AC$,$\angle B = 60^{\circ}$,$AD\perp BC$ 于点 $D$,$P$ 是 $AD$ 上的一个动点,$PE\perp AC$ 于点 $E$,连接 $CP$。若 $AD = 16$,则 $PC + PE$ 的最小值是
4
。
答案:
14.4 [解析]分类讨论:①当△PQB≌△CPA时,BP=AC=4m,则QB=AP=AB−BP=16−4=12(m),点P的运动时间是4÷1=4(min),点Q的运动时间是12÷3=4(min),
∴当t=4min时,两个三角形全等.②当△QPB≌△CPA时,BQ=AC=4m,AP=BP=16÷2=8(m),则点P运动的时间是8÷1=8(min),点Q运动的时间是4÷3=$\frac{4}{3}$(min),故不能成立.综上所述,运动4min后,△CPA与△PQB全等.
∴当t=4min时,两个三角形全等.②当△QPB≌△CPA时,BQ=AC=4m,AP=BP=16÷2=8(m),则点P运动的时间是8÷1=8(min),点Q运动的时间是4÷3=$\frac{4}{3}$(min),故不能成立.综上所述,运动4min后,△CPA与△PQB全等.
查看更多完整答案,请扫码查看


