2025年全程检测单元测试卷八年级数学上册沪教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年全程检测单元测试卷八年级数学上册沪教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
9. 某班学生在研究弹簧的长度跟外力的变化关系时, 实验记录得到相应数据, 如下表:

则下列图象中, 能表示 $ y $ 与 $ x $ 之间的函数关系的大致图象是(
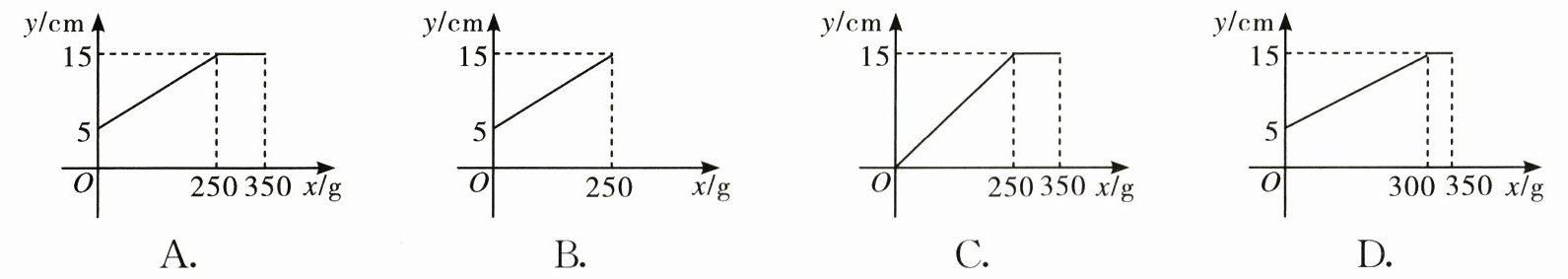
A.
B.
C.
D.

则下列图象中, 能表示 $ y $ 与 $ x $ 之间的函数关系的大致图象是(
A
).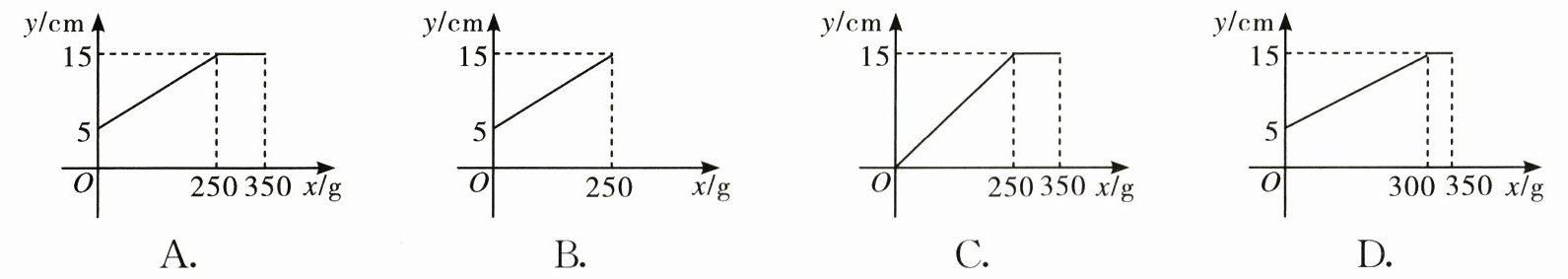
A.
B.
C.
D.
答案:
9.A 【解析】根据表格信息可知,当0 < x < 250时,砝码质量每增加50g,则弹簧长度增加2cm,符合一次函数的要求.设y = kx + b,把点(0,5),(50,7)代入,得$\begin{cases}b = 5,\\50k + b = 7.\end{cases}$解得$\begin{cases}k = \frac{1}{25},\\b = 5.\end{cases}$即当0 < x < 250时,函数表达式为y = $\frac{1}{25}x + 5$.当250 ≤ x ≤ 350时,y = 15.四个选项中,只有选项A的图象符合题意,故选A.
10. “复兴号”动车是我国具有完全自主知识产权、达到世界先进水平的中国标准动车组. 假设“复兴号”动车组从甲站驶出 $ 10\,km $ 到达乙处后, 以 $ 350\,km/h $ 的速度匀速前进. 设列车离开乙处 $ t\,h $ 后, 其离甲站的路程为 $ s\,km $, 则 $ s $ 与 $ t $ 之间的函数表达式为(
A.$ s = 350t $
B.$ s = 350t - 10 $
C.$ s = 350t + 10 $
D.$ s = 10t + 350 $
C
).A.$ s = 350t $
B.$ s = 350t - 10 $
C.$ s = 350t + 10 $
D.$ s = 10t + 350 $
答案:
10.C 【解析】列车到达乙处时已经离甲站10km,再根据公式“路程 = 速度×时间”得s = 350t + 10.故选C.
11. 一次函数 $ y = k_1x + b $ ( $ k_1,b $ 为常数) 与 $ y = k_2x + a $ ( $ k_2,a $ 为常数) 的图象如图3所示, 则关于 $ x,y $ 的方程组 $ \begin{cases}y = k_1x + b,\\y = k_2x + a\end{cases} $ 的解是

$\begin{cases}x = 4,\\y = - 6\end{cases}$
.
答案:
11.$\begin{cases}x = 4,\\y = - 6\end{cases}$【解析】两个函数图象的交点坐标即为所求方程组的解,根据图象可直接得出答案.
12. 一辆汽车在行驶过程中, 行驶路程 $ y\,km $ 和行驶时间 $ x\,h $ 之间的函数关系如图4所示. 当 $ 0 \leq x \leq 0.5 $ 时, $ y = 50x $; 当 $ 0.5 < x \leq 2 $ 时, $ y $ 与 $ x $ 之间的函数表达式为

y = 80x - 15
.
答案:
12.y = 80x - 15 【解析】把x = 0.5代入y = 50x,得y = 25,所以两线段重合点的坐标为(0.5,25).当0.5 < x ≤ 2时,设y = kx + b,把点(0.5,25),(2,145)代入,得$\begin{cases}0.5k + b = 25,\\2k + b = 145.\end{cases}$解得$\begin{cases}k = 80,\\b = - 15.\end{cases}$所以当0.5 < x ≤ 2时,y = 80x - 15.
13. 如图5, 一次函数 $ y = kx + b $ 的图象与 $ x $ 轴的交点坐标为 $ (2,0) $, 现有下列说法: ① $ y $ 随 $ x $ 的增大而减小; ② $ b > 0 $; ③关于 $ x $ 的方程 $ kx + b = 0 $ 的解为 $ x = 2 $. 其中正确的说法有
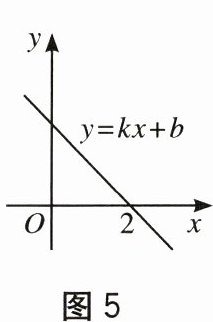
①②③
(填序号).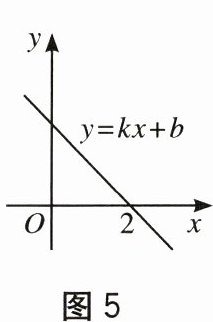
答案:
13.①②③ 【解析】因为一次函数的图象经过第一、二、四象限,所以y随x的增大而减小,故①说法正确;因为一次函数的图象与y轴的交点在正半轴上,所以b > 0,故②说法正确;因为一次函数的图象与x轴的交点为(2,0),所以当y = 0时,x = 2,即关于x的方程kx + b = 0的解为x = 2,故③说法正确.所以答案为①②③.
14. 小明在实践课中用长度相同的小木棒按图6所示的规律拼图案, 其中第①个图案用了9根小木棒, 第②个图案用了14根小木棒, 第③个图案用了19根小木棒, 第④个图案用了24根小木棒……按此规律排列下去, 若用 $ x $ 表示图案的序号, $ y $ 表示小木棒的数量, 则 $ y $ 与 $ x $ 之间的函数表达式为

y = 5x + 4
.
答案:
14.y = 5x + 4 【解析】观察图形可得,图案①的小木棒数为4 + 5,图案②的小木棒数为4 + 5×2,图案③的小木棒数为4 + 5×3……则第x个图案的小木棒数为4 + 5×x.所以y = 5x + 4.
查看更多完整答案,请扫码查看


