《2025年全程助学与学习评估九年级数学上册浙教版》

1. 已知实数 $ x $,$ y $ 适合 $ x^{2}+y+4x - 1 = 0 $,则 $ y $ 的最大值为5。

答案： 5（题目空缺为填数题则无需填写选项）。

2. 函数 $ y = x^{2}-4x + 3(-3\leqslant x\leqslant 3) $ 的最小值是-1,最大值是24。

答案： 最小值是-1，最大值是24 ，（按照横线顺序）故填-1；24。

3. 已知直角三角形的两直角边之和为 $ 2 $,则斜边长可能达到的最小值是$\sqrt{2}$。

答案： $\sqrt{2}$（或 对应的填空答案，如“$\sqrt{2}$”或“根号2”等，根据题目要求填写）

4. 一件工艺品进价为 $ 100 $ 元,以标价 $ 135 $ 元售出,每天可售出 $ 100 $ 件。根据销售统计,一件工艺品每降价 $ 1 $ 元出售,则每天可多售出 $ 4 $ 件,要使每天获得的利润最大,每件需降价5元。

答案： 5

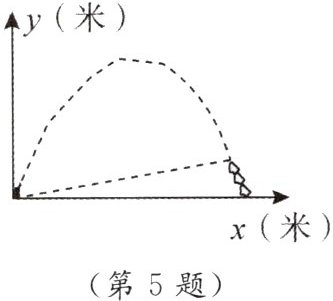
5. 如图,某广场有一喷水池,水从地面喷出,以水平地面为 $ x $ 轴,出水点为原点,建立平面直角坐标系,水在空中划出的曲线是抛物线 $ y = -x^{2}+5x $(单位：米)的一部分。求水喷出的最大高度和最大的水平距离。

答案： 求水喷出的最大高度：
对于抛物线 $ y = -x^2 + 5x $，其中 $ a = -1 $，$ b = 5 $，$ c = 0 $。
因为 $ a = -1 ＜ 0 $，抛物线开口向下，顶点为最高点。
顶点的横坐标为：
$ x = -\frac{b}{2a} = -\frac{5}{2 × (-1)} = \frac{5}{2} $
将 $ x = \frac{5}{2} $ 代入抛物线方程，得最大高度：
$ y = -\left(\frac{5}{2}\right)^2 + 5 × \frac{5}{2} = -\frac{25}{4} + \frac{25}{2} = \frac{25}{4} = 6.25 \, 米 $
求最大的水平距离：
令 $ y = 0 $，即 $ -x^2 + 5x = 0 $。
解方程：
$ x(-x + 5) = 0 $
得 $ x_1 = 0 $（出水点），$ x_2 = 5 $（落水点）。
最大水平距离为 $ x_2 - x_1 = 5 - 0 = 5 \, 米 $。
结论：水喷出的最大高度为 $ 6.25 $ 米，最大水平距离为 $ 5 $ 米。

6. 某商品的进价为每件 $ 30 $ 元,现在的售价为每件 $ 40 $ 元,每星期可卖出 $ 150 $ 件。市场调查反映：若每件的售价每涨 $ 1 $ 元(售价每件不能高于 $ 45 $ 元),则每星期少卖 $ 10 $ 件。设每件涨价 $ x $ 元($ x $ 为非负整数),每星期的销量为 $ y $ 件。
(1) 求 $ y $ 与 $ x $ 的函数表达式及自变量 $ x $ 的取值范围。
(2) 设利润为 $ W $ 元,写出 $ W $ 与 $ x $ 的函数表达式。

答案：
(1) 由题意得，每件涨价 $ x $ 元，每星期少卖 $ 10x $ 件，所以销量 $ y = 150 - 10x $。
因为售价每件不能高于 45 元，所以 $ 40 + x \leq 45 $，即 $ x \leq 5 $，又 $ x $ 为非负整数，故 $ 0 \leq x \leq 5 $ 且 $ x $ 为整数。
函数表达式：$ y = -10x + 150 $，自变量取值范围：$ 0 \leq x \leq 5 $（$ x $ 为整数）。
(2) 每件利润为 $ (40 + x - 30) = (10 + x) $ 元，销量为 $ y = -10x + 150 $，
所以利润 $ W = (10 + x)(-10x + 150) $，展开得 $ W = -10x^2 + 50x + 1500 $。
函数表达式：$ W = -10x^2 + 50x + 1500 $（$ 0 \leq x \leq 5 $，$ x $ 为整数）。