《2025年全程助学与学习评估九年级数学上册浙教版》

8. 如图,已知 $ \odot O $ 的直径 $ AB = 6 $,$ E $,$ F $ 为 $ AB $ 的三等分点,$ M $,$ N $ 为 $ \overset{\frown}{AB} $ 上两点,且 $ \angle MEB = \angle NFB = 60° $,则 $ EM + FN = $√33。

答案： √33

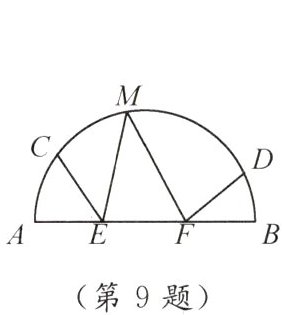
9. 如图,$ AB $ 是半 $ \odot O $ 的直径,$ C $,$ D $,$ M $ 是半圆弧上的点,且 $ \overset{\frown}{AC} = 50° $,$ \overset{\frown}{BD} = 20° $.$ E $,$ F $ 在直径 $ AB $ 上,且 $ \angle AEC = \angle FEM $,$ \angle BFD = \angle EFM $,则 $ \angle M $ 的度数为(B)

A.$ 25° $
B.$ 35° $
C.$ 45° $
D.$ 55° $

答案： B

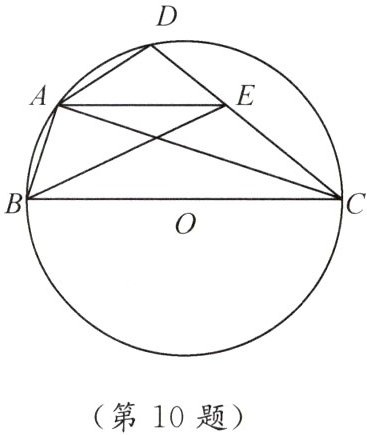
10. 如图,设四边形 $ ABCD $ 内接于 $ \odot O $,$ BC $ 为 $ \odot O $ 的直径,$ E $ 为 $ DC $ 上一点,若 $ AE // BC $,$ AE = EC = 5 $,$ AB = 4 $。
求：(1) $ AD $ 的长。
(2) $ \odot O $ 的半径。
(3) $ \triangle ABE $ 的面积。

答案：
(1) 设 $ BC = 2r $，以 $ BC $ 为x轴，圆心 $ O $ 为原点建立坐标系，则 $ B(-r,0) $，$ C(r,0) $，圆方程 $ x^2 + y^2 = r^2 $。
因 $ AE // BC $，设 $ A(x_1,y_1) $，则 $ E(x_1+5,y_1) $（$ AE=5 $）。
由 $ AB=4 $，得 $ (x_1 + r)^2 + y_1^2 = 16 $，又 $ x_1^2 + y_1^2 = r^2 $，联立得 $ x_1 = \frac{8 - r^2}{r} $。
由 $ EC=5 $，$ E(x_1+5,y_1) $，$ C(r,0) $，得 $ (r - (x_1 + 5))^2 + y_1^2 = 25 $，代入 $ y_1^2 = r^2 - x_1^2 $ 及 $ x_1 = \frac{8 - r^2}{r} $，解得 $ r=5 $。
此时 $ x_1 = -\frac{17}{5} $，$ y_1 = \frac{4\sqrt{21}}{5} $，$ E\left(\frac{8}{5},\frac{4\sqrt{21}}{5}\right) $。
直线 $ DC $ 方程：$ y = -\frac{4\sqrt{21}}{17}(x - 5) $，与圆方程联立得 $ D\left(\frac{47}{125},\frac{136\sqrt{21}}{125}\right) $。
$ A\left(-\frac{17}{5},\frac{4\sqrt{21}}{5}\right) $，$ AD = \sqrt{\left(\frac{47}{125} + \frac{425}{125}\right)^2 + \left(\frac{136\sqrt{21}}{125} - \frac{100\sqrt{21}}{125}\right)^2} = 4 $。
(2) 由
(1)知 $ r=5 $。
(3) $ A\left(-\frac{17}{5},\frac{4\sqrt{21}}{5}\right) $，$ B(-5,0) $，$ E\left(\frac{8}{5},\frac{4\sqrt{21}}{5}\right) $，$ AE=5 $，高为 $ \frac{4\sqrt{21}}{5} $，面积 $ S = \frac{1}{2} × 5 × \frac{4\sqrt{21}}{5} = 2\sqrt{21} $。
(1) $ 4 $
(2) $ 5 $
(3) $ 2\sqrt{21} $