《2025年全程助学与学习评估九年级数学上册浙教版》

7. 函数 $ y = mx^{m^{2}-2m - 1} $ 是二次函数,当 $ m = $3时,其图象开口向上；当 $ m = $-1时,其图象开口向下。

答案：
第一个空填：3
第二个空填：-1

8. 抛物线 $ y = - 2x^{2} $ 上一点到 $ x $ 轴的距离是 $ 8 $,则该点的横坐标是(D)
A.$ - 64 $
B.$ 2 $
C.$ - 2 $
D.$ - 2 $ 或 $ 2 $

答案： D

9. 已知二次函数 $ y = ax^{2}(a \neq 0) $ 的图象与反比例函数 $ y = - \frac{8}{x} $ 的图象交点的横坐标为 $ - 2 $。判断点 $ A(\sqrt{2}, - 2) $,$ B( - 3,9) $ 是否在这个二次函数的图象上？

答案： 当$x = -2$时，代入反比例函数$y=-\frac{8}{x}$，得$y=-\frac{8}{-2}=4$，所以交点坐标为$(-2,4)$。
将$(-2,4)$代入二次函数$y = ax^{2}$，得$4=a×(-2)^{2}$，即$4a = 4$，解得$a = 1$，所以二次函数解析式为$y=x^{2}$。
对于点$A(\sqrt{2},-2)$，当$x=\sqrt{2}$时，$y=(\sqrt{2})^{2}=2\neq -2$，所以点$A$不在二次函数图象上。
对于点$B(-3,9)$，当$x=-3$时，$y=(-3)^{2}=9$，所以点$B$在二次函数图象上。
结论：点$A$不在，点$B$在。

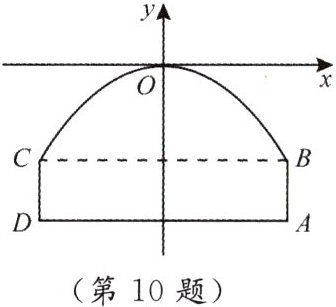
10. 如图,隧道的截面由抛物线 $ BOC $ 和矩形 $ ABCD $ 构成,矩形的长 $ AD $ 为 $ 8m $,宽 $ AB $ 为 $ 2m $,以过顶点 $ O $ 且平行于 $ AD $ 的直线为 $ x $ 轴,线段 $ AD $ 的中垂线为 $ y $ 轴,建立平面直角坐标系,抛物线顶点 $ O $ 到 $ AD $ 的距离为 $ 5m $。
(1) 求这条抛物线的函数表达式。
(2) 如果隧道是双向通道,现有一辆货车高 $ 3.6m $,宽 $ 2.4m $,这辆货车能否通过该隧道？请通过计算进行说明。

答案： 1. （1）
解：已知抛物线顶点$O(0,0)$，设抛物线的函数表达式为$y = ax^{2}(a\neq0)$。
因为$AD = 8m$，$AB = 2m$，抛物线顶点$O$到$AD$的距离为$5m$，所以点$B$的坐标为$(4, - 3)$（$y$轴下方为负）。
把$B(4, - 3)$代入$y = ax^{2}$中，得$-3=a×4^{2}$，即$16a=-3$，解得$a =-\frac{3}{16}$。
所以这条抛物线的函数表达式为$y =-\frac{3}{16}x^{2}$。
2. （2）
解：已知货车宽$2.4m$，则$x=\pm1.2$。
把$x = 1.2$代入$y =-\frac{3}{16}x^{2}$中，得$y=-\frac{3}{16}×1.2^{2}=-\frac{3}{16}×1.44=-0.27$。
此时货车顶部距离$AD$的高度为$5-(|y| + 2)$，$\vert y\vert=0.27$，则$5-(0.27 + 2)=2.73m$。
因为$2.73m\gt3.6m$。
所以：
(1) 抛物线的函数表达式为$y =-\frac{3}{16}x^{2}$；
(2) 这辆货车能通过该隧道。