1. 半径为 $ r $ 的圆内接正三角形的边长为
√3 r
,面积为3√3 r²/4
。
答案:
√3 r;3√3 r²/4
2. 半径为 $ 2cm $ 的圆内接正六边形的周长为
12
$ cm $,面积为6√3
$ cm^2 $。
答案:
12,6√3
3. 圆内接正方形 $ ABCD $ 的边长为 $ 2 $,弦 $ AE $ 平分 $ BC $ 边,与 $ BC $ 交于 $ F $,则弦 $ AE $ 的长为
6√5/5
。
答案:
6√5/5
4. 如图,半径为 $ 3 $ 的圆内接正八边形 $ ABCDEFGH $,则弦 $ AG $ 的长为
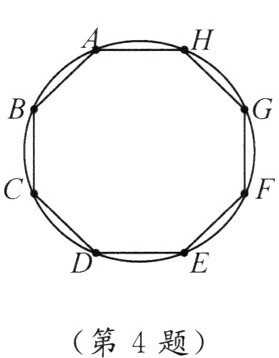
3√2
。
答案:
3√2
5. 如图,在扇形 $ OAB $ 中,$ \angle AOB = 110° $,半径 $ OA = 18 $,将扇形 $ OAB $ 沿过点 $ B $ 的直线折叠,点 $ O $ 恰好落在 $ \overset{\frown}{AB} $ 上的点 $ D $ 处,折痕交 $ OA $ 于点 $ C $,则 $ \overset{\frown}{AD} $ 的长为
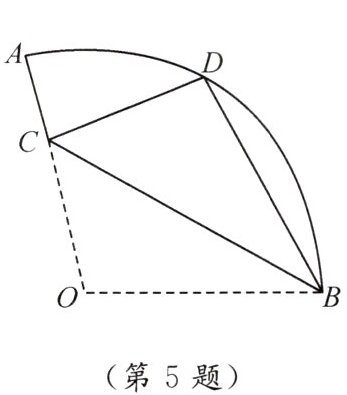
5π
。
答案:
5π
6. 如图,有一圆通过 $ \triangle ABC $ 的三个顶点,且 $ BC $ 的中垂线与圆相交于 $ D $ 点。若 $ \angle B = 74° $,$ \angle C = 46° $,则 $ \overset{\frown}{AD} $ 的度数为(
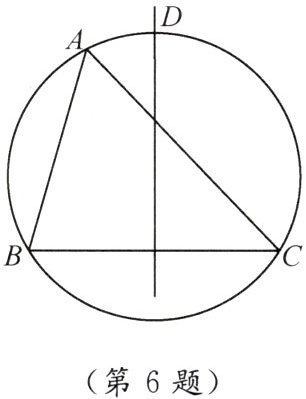
A.$ 23° $
B.$ 28° $
C.$ 30° $
D.$ 37° $
B
)
A.$ 23° $
B.$ 28° $
C.$ 30° $
D.$ 37° $
答案:
B
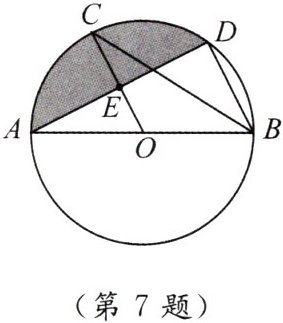
7. 如图,已知 $ AB $ 是 $ \odot O $ 的直径,$ C $,$ D $ 是 $ \odot O $ 上的点,$ OC // BD $,交 $ AD $ 于点 $ E $,连结 $ BC $。
(1) 求证:$ AE = ED $。
(2) 若 $ AB = 6 $,$ \angle CBD = 30° $,求图中阴影部分的面积。
(1) 求证:$ AE = ED $。
(2) 若 $ AB = 6 $,$ \angle CBD = 30° $,求图中阴影部分的面积。

答案:
(1) 见证明;
(2) $\frac{3\pi}{2}$
(1) 见证明;
(2) $\frac{3\pi}{2}$
查看更多完整答案,请扫码查看


