《2025年课时特训六年级数学上册人教版》

3. 一个圆形池塘的半径是25米,在它的周围铺一条环形水泥路,路宽3米。水泥路面的面积是多少平方米？

答案：

外圆半径：$25 + 3 = 28$（米）

环形面积：$\pi × (28^2 - 25^2) = \pi × (784 - 625) = \pi × 159 = 159 × 3.14 = 499.26$（平方米）

4. 如下图,小华和小明分别沿着弧线跑,你能求出他们跑的路程相差多少米吗？

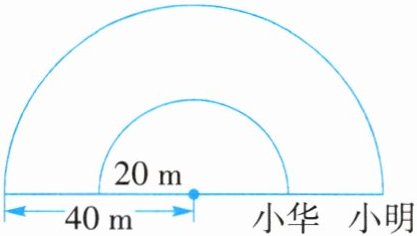
答案：

小明跑的路程：$\frac{1}{2} × 2 × \pi × 40 = 40\pi$（米）

小华跑的路程：$\frac{1}{2} × 2 × \pi × 20 = 20\pi$（米）

路程差：$40\pi - 20\pi = 20\pi$

$20\pi = 20 × 3.14 = 62.8$（米）

5. 公园里有一个圆形的养鱼池,量得养鱼池的周长是100.48米,养鱼池的中间有一个圆形小岛,半径是6米。这个养鱼池的水域面积是多少？

答案：

养鱼池的半径：$100.48÷3.14÷2 = 16$（米）

水域面积：$3.14×(16^{2}-6^{2})=3.14×(256 - 36)=3.14×220 = 690.8$（平方米）

答：这个养鱼池的水域面积是$690.8$平方米。

6. 如图,大正方形的面积比小正方形的面积多$10 cm^2,$求圆在两正方形之间部分的面积。

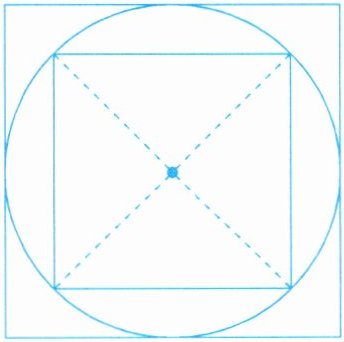
答案： 解：设圆的半径为$r$。
由题意：$4r^2 - 2r^2=10$，得$2r^2=10$，$r^2=5$。
圆面积为$\pi r^2=5\pi$。
两正方形之间部分面积：$5\pi - 10\approx5×3.14 - 10=15.7 - 10=5.7\,cm^2$。