《2025年新课标学习方法指导丛书七年级数学上册浙教版》

25. (2分)如图,正方形$ABCD$的边长为100米,甲、乙两个动点分别从点$A和点B$同时出发按逆时针方向移动。甲的速度是7米/秒,乙的速度是10米/秒,经过70秒,甲、乙两动点第一次位于正方形的同一条边上。

答案： 70

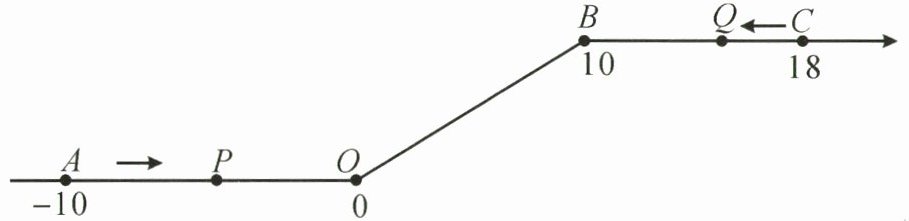
26. (6分)如图,将一条数轴在原点$O和点B$处各折一下,得到一条“折线数轴”。图中点$A$表示-10,点$B$表示10,点$C$表示18,我们称点$A和点C$在数轴上相距28个单位长度。动点$P从点A$出发,以2个单位长度/秒的速度沿着“折线数轴”的正方向运动,从点$O运动到点B$期间速度变为原来的一半,之后立刻恢复原速；同时,动点$Q从点C$出发,以1个单位长度/秒的速度沿着数轴的负方向运动,从点$B运动到点O$期间速度变为原来的两倍,之后也立刻恢复原速。设运动的时间为$t$秒。问：

(1)动点$P从点A运动至点C$需要多少时间？
(2)$P$,$Q$两点相遇时,求出相遇点$M$所对应的数是多少。
(3)求当$t$为何值时,$P$,$O两点在数轴上相距的长度与Q$,$B$两点在数轴上相距的长度相等。

答案：
(1)
P从A到C路径：A→O→B→C。
A→O：距离10，速度2单位/秒，时间$ t_1=\frac{10}{2}=5 $秒；
O→B：距离10，速度1单位/秒（原速一半），时间$ t_2=\frac{10}{1}=10 $秒；
B→C：距离8，速度2单位/秒，时间$ t_3=\frac{8}{2}=4 $秒。
总时间$ t=5+10+4=19 $秒。
(2)
P、Q运动阶段及位置公式：
P：
AO段（0≤t≤5）：$ x_P=-10+2t $；
OB段（5＜t≤15）：$ x_P=t-5 $；
BC段（t＞15）：$ x_P=2t-20 $。
Q：
CB段（0≤t≤8）：$ x_Q=18-t $；
BO段（8＜t≤13）：$ x_Q=26-2t $；
OA段（t＞13）：$ x_Q=13-t $。
相遇时$ x_P=x_Q $，经分析在8＜t≤13（P在OB，Q在BO）：
$ t-5=26-2t $，解得$ t=\frac{31}{3} $。
相遇点$ M=x_P=\frac{31}{3}-5=\frac{16}{3} $。
(3)
$|x_P|=|x_Q-10|$，分阶段讨论：
1. P在AO（0≤t≤5），Q在CB（0≤t≤8）：$ 10-2t=8-t $→$ t=2 $；
2. P在OB（5＜t≤15），Q在CB（0≤t≤8）：$ t-5=8-t $→$ t=6.5 $；
3. P在OB（5＜t≤15），Q在BO（8＜t≤13）：$ t-5=2t-16 $→$ t=11 $；
4. P在BC（t＞15），Q在OA（t＞13）：$ 2t-20=t-3 $→$ t=17 $。
综上，$ t=2 $，$ 6.5 $，$ 11 $，$ 17 $。
答案
(1) 19秒
(2) $\frac{16}{3}$
(3) $ t=2 $，$ 6.5 $，$ 11 $，$ 17 $