《2025年新课标学习方法指导丛书七年级数学上册浙教版》

26.(2分)我国古代《易经》一书中记载了一种“结绳计数”的方法：一女子在从右到左依次排列的绳子上打结,满六进一,用来记录采集到的野果数量。下列图示中表示91颗的是(A)

答案： A

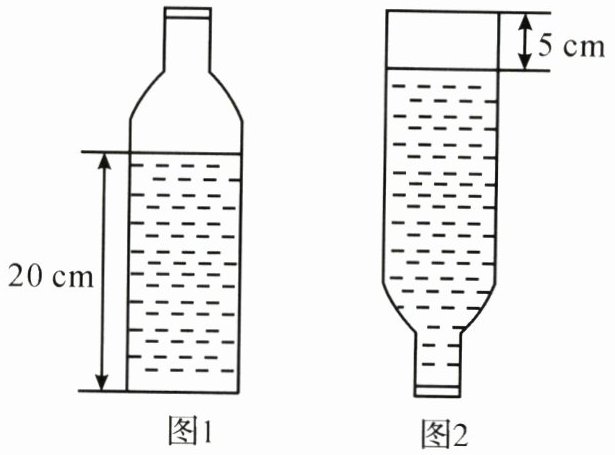
27.(6分)一个长12cm、宽12cm、高8cm的长方体容器中装满了水。小明先把容器中的水倒满2个底面半径为3cm,高为5cm的圆柱体杯子,再把剩下的水全部倒入瓶子甲中。瓶子甲正放时如图1,瓶内溶液的高度为20cm；瓶子甲倒放时如图2,空余部分的高度为5cm。(π取3,容器的厚度不计)
(1)求瓶子甲的底面积。
(2)求瓶子甲的容积。

答案：
(1) 长方体容器的体积：
$ V_{长方体} = 12 × 12 × 8 = 1152 cm^3 $。
2 个圆柱体杯子的体积：
$ V_{圆柱体} = 2 × \pi r^2 h = 2 × 3 × 3^2 × 5 = 270 cm^3 $。
剩余水的体积：
$ V_{剩余} = V_{长方体} - V_{圆柱体} = 1152 - 270 = 882 cm^3 $。
设瓶子甲的底面积为 $ S $，则：
$ 20S = 882 $。
$ S = \frac{882}{20} = 44.1 cm^2 $。
答：底面积为$44.1 cm^2 $。
(2) 瓶子甲的容积：
$ V_{瓶子甲} = 20S + 5S = 25S = 25 × 44.1 = 1102.5 cm^3 $。
答：容积为$1102.5 cm^3 $。