第60页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
26. (6分)由面积都是1的小正方形组成的方格平面叫作格点平面,纵横两组平行线的交点为格点,如图1中有9个格点。如果一个正方形的每个顶点都在格点上,那么这个正方形称为“格点正方形”。
【探索发现】
(1)观察图形完成下表:
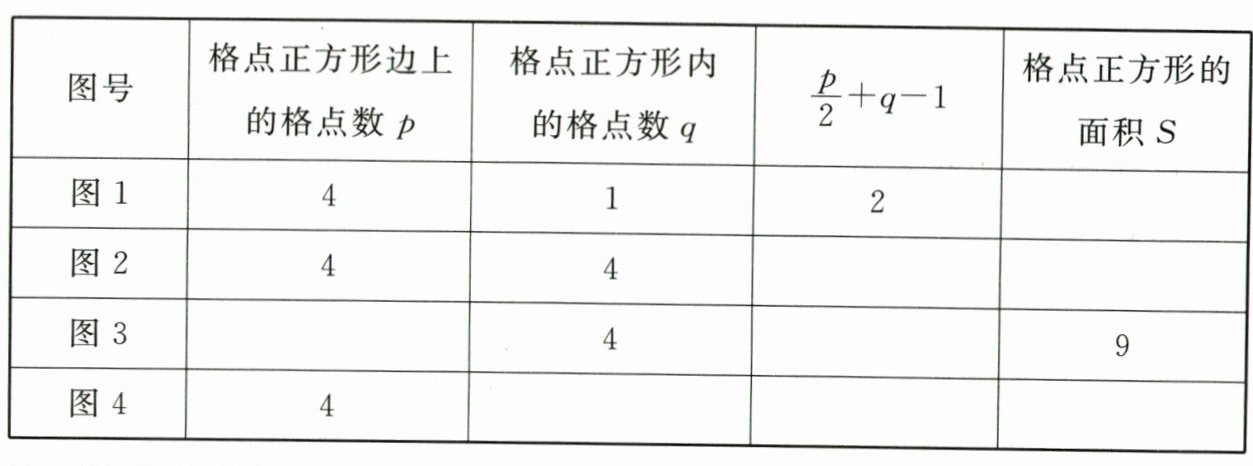
从上述表格中你发现S与p,q之间有什么关系?
【继续猜想】
(2)类比格点正方形的概念,如果一个长方形的每个顶点都在格点上,那么这个长方形称为格点长方形。对于格点长方形的面积,你认为有类似(1)中的结论吗?试以图5中格点长方形为例来验证。
【学以致用】
(3)在图6中画一个格点三角形,使它的面积为5.5,且这个三角形内的格点数最多。
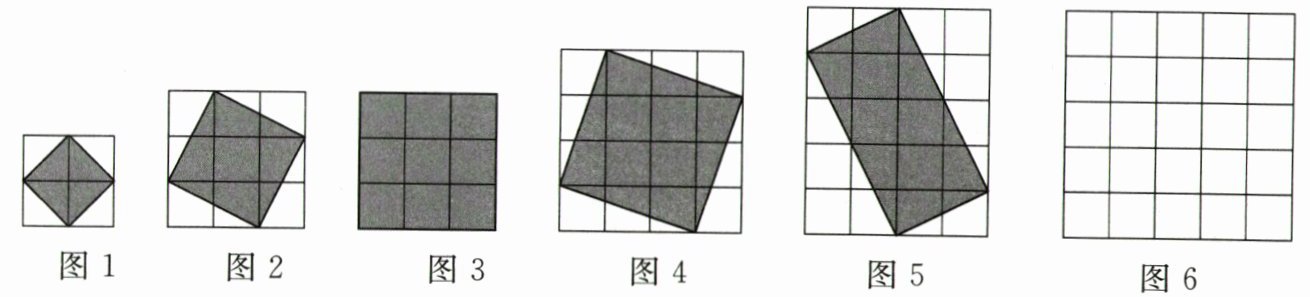
【探索发现】
(1)观察图形完成下表:

从上述表格中你发现S与p,q之间有什么关系?
【继续猜想】
(2)类比格点正方形的概念,如果一个长方形的每个顶点都在格点上,那么这个长方形称为格点长方形。对于格点长方形的面积,你认为有类似(1)中的结论吗?试以图5中格点长方形为例来验证。
【学以致用】
(3)在图6中画一个格点三角形,使它的面积为5.5,且这个三角形内的格点数最多。

答案:
(1)
|图号|格点正方形边上的格点数p|格点正方形内的格点数q|$\frac{p}{2}+q-1$|格点正方形的面积S|
|----|----|----|----|----|
|图1|4|1|2|2|
|图2|4|4|5|5|
|图3|12|4|9|9|
|图4|4|7|8|8|
关系:$S=\frac{p}{2}+q-1$
(2)有类似结论,格点长方形的面积$S=\frac{p}{2}+q-1$。
验证:设图5中格点长方形边界格点数为$p$,内部格点数为$q$,经观察得$p=10$,$q=2$,则$\frac{p}{2}+q-1=\frac{10}{2}+2-1=5+2-1=6$,该长方形面积为$6$(长3宽2),故$S=\frac{p}{2}+q-1$成立。
(3)(画图略,描述:顶点为格点,例如取$(0,0)$,$(4,0)$,$(1,3)$,构成三角形,内部格点数最多为5)
(1)
|图号|格点正方形边上的格点数p|格点正方形内的格点数q|$\frac{p}{2}+q-1$|格点正方形的面积S|
|----|----|----|----|----|
|图1|4|1|2|2|
|图2|4|4|5|5|
|图3|12|4|9|9|
|图4|4|7|8|8|
关系:$S=\frac{p}{2}+q-1$
(2)有类似结论,格点长方形的面积$S=\frac{p}{2}+q-1$。
验证:设图5中格点长方形边界格点数为$p$,内部格点数为$q$,经观察得$p=10$,$q=2$,则$\frac{p}{2}+q-1=\frac{10}{2}+2-1=5+2-1=6$,该长方形面积为$6$(长3宽2),故$S=\frac{p}{2}+q-1$成立。
(3)(画图略,描述:顶点为格点,例如取$(0,0)$,$(4,0)$,$(1,3)$,构成三角形,内部格点数最多为5)
查看更多完整答案,请扫码查看


