《2025年同步练习江苏七年级数学上册苏科版》

9. 计算：
(1)48°39′+67°31′；
(2)61°39′-22°5′32″；
(3)21°17′×6；
(4)65°24′÷4.

答案： （1）48°39'+67°31'=115°70'=116°10' （2）61°39'-22°5'32''=61°38'60''-22°5'32''=39°33'28'' （3）21°17'×6=126°102'=127°42' （4）65°24'÷4=16.25°6'=16°21'

10. 如图,O,A,B,C,D都为格点,∠AOB= ∠α,∠COD= ∠β.

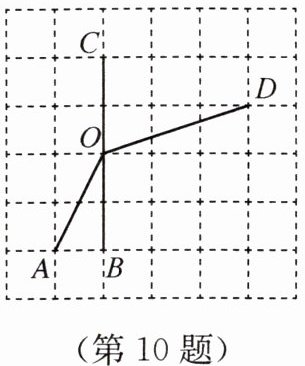
(1)在图中找出一个格点E,连接OE,使得∠DOE= ∠α+∠β；
(2)在图中找出一个格点F,连接OF,使得∠DOF= ∠β-∠α.

答案：
如图

11. (1)数学活动课上,李老师让同学们准备一副三角板,并利用它们画出一些角,例如30°,45°,60°,90°. 小明利用三角板画出了一个120°的角. 小乐利用三角板画出了一个15°的角. 你还能用三角板画出多少度的角？
(2)如图,李老师将两个三角板放置在一起,于是产生了新的数学问题. ∠AOB= ∠DCO= 90°,∠A= 45°,∠DOC= 30°,在∠BOD,∠AOC(∠BOD≤180°,∠AOC≤180°)内作射线OP,OQ,且∠POB= 2∠DOP,∠QOA= 2∠QOC. 求∠POQ的度数.

答案： （1）用三角板还能作出75°和105°的角,等等 （2）因为∠AOB=90°,∠COD=30°,所以∠BOD+∠AOC=360°-∠AOB-∠DOC=240°,因为∠POB=2∠DOP,∠QOA=2∠QOC,所以∠DOP= $\frac{1}{3}$∠BOD,∠QOC= $\frac{1}{3}$∠AOC,所以∠DOP+∠QOC= $\frac{1}{3}$(∠BOD+∠AOC)=80°,因为∠POQ=∠DOP+∠QOC+∠COD,∠COD=30°,所以∠POQ=80°+30°=110°