《2025年同步练习江苏七年级数学上册苏科版》

8. 用字母表示下列运算或数量关系：
(1)某个数的2倍与5的差；
(2)一个数的相反数与2的平方的和大于3.

答案：
(1) $2a-5$
(2) $-a+2^{2}＞3$

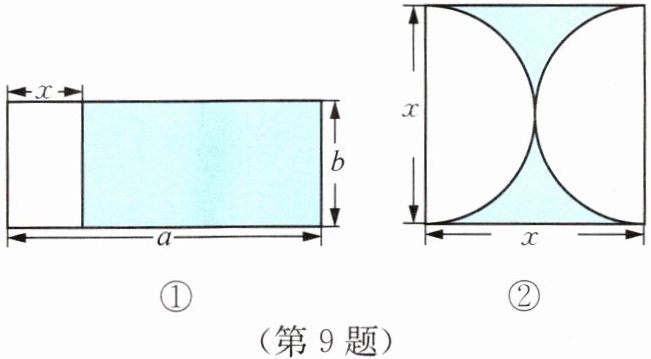
9. 用字母表示图中阴影部分的面积：

(第9题)
图①中S阴影=$(a-x)b$,图②中S阴影=$\left(1-\frac{\pi}{4}\right)x^{2}$.

答案： $(a-x)b,\left(1-\frac{\pi}{4}\right)x^{2}$

10. 观察下列各式：$2^2 - 2×1= 1+1$,$3^2 - 2×2= 4+1$,$4^2 - 2×3= 9+1$,$5^2 - 2×4= 16+1$,…,第n个等式是$(n+1)^{2}-2^{n}=n^{2}+1$.

答案： $(n+1)^{2}-2^{n}=n^{2}+1$

11. 观察下面两个算式并回答问题：
① $63×67= 6×(6+1)×100+3×7= 4200+21= 4221$；
② $692×698= 69×(69+1)×100+2×8= 483000+16= 483016$.
(1)上述算式中,两个因数个位上的数字之和是多少？其余各位上的数字有什么特征？
(2)猜想符合上述特征的两数相乘的计算方法,并举例验证.

答案：
(1) 10,对应相同
(2) 如果两个数个位上数字之和为10,其余数位上数字相同,记其余数位上数字组成的数为 k,个位上数字为 m,n,那么这两个数之积等于 $k×(k+1)×100+m× n$.例如,1 234×1 236=123×(123+1)×100+4×6=15 252 024

12. 将奇数1至2025按照顺序排成下表：

记$P_{mn}$表示第m行第n个数,如$P_{23}= 17$表示第2行第3个数是17.
(1)$P_{43}=$41；
(2)$P_{mn}=$$12(m-1)+2(n-1)+1$(用含m,n的代数式表示).

答案：
(1) 41
(2) 形式不唯一,如 $12(m-1)+2(n-1)+1$(注:不需要化简)