《2025年同步练习江苏七年级数学上册苏科版》

9. 魔术师说：“请你任想一个两位数,将十位数字乘2,然后加3,将所得新数乘5,最后将得到的数加个位数字,只要告诉我计算结果,我就能知道你心里想的两位数.”请你解释这个魔术背后的数学道理.

答案： 设这个数为$\overline{ab}$,则计算结果为$(2a+3)×5+b=10a+b+15$,只要将结果减15,就得到$10a+b$,即为原来的两位数

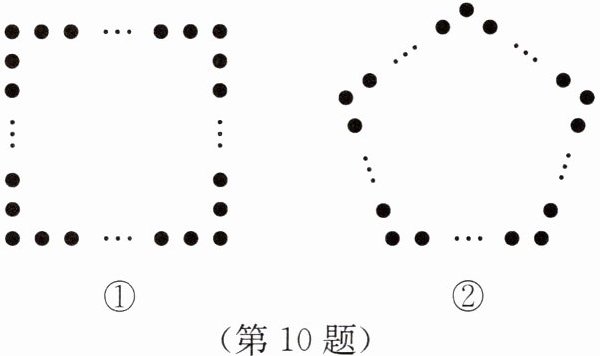
10. (1)如图①,正方形的每条边上都有$n$个棋子,图①中共有多少个棋子？
(2)如图②,正五边形(五条边相等的五边形)的每条边上都有$n$个棋子,图②比图①多几个棋子？
(3)正$m$边形(每条边都相等的$m$边形)的每条边上都有$n$个棋子,则共有多少个棋子？

答案：

解：$(1)$图$①$中共有$4(n-1)$个棋子$.$　　

$(2)$图$②$中有$5(n-1)$个棋子，　　

图$②$比图$①$中多$5(n-1)-4(n-1)=(n-1)$个棋子$.$　　

$(3)$正$m $边形共有$m(n-1)$个棋子$.$　　

11. 课堂上,老师设计了一个数学游戏,给甲、乙、丙三名同学各一张写有代数式(已化简)的卡片,若两位同学的代数式相减等于第三位同学的代数式,则游戏成功.甲、乙、丙的卡片如图所示,其中丙的卡片有一部分看不清楚了(图中阴影所示).

(1)计算甲的代数式减乙的代数式的结果，并判断该运算能否使游戏成功;

(2)小明发现丙的代数式减甲的代数式可以使游戏成功，请求出丙的代数式.

答案：

解：$(1)$甲$-$乙$=2a^2+4ab+3-(-\frac 12a^2-6ab+9)=2a^2+4ab+3+\frac 12a^2+6ab-9$　　

$=\frac 52a^2+10ab-6.$　　

因为丙为$+12，$　　

所以游戏不成功$.$　　

$(2)$由题意得丙$-$甲$=$乙，　　

所以丙$=$甲$+$乙$=2a^2+4ab+3+(-\frac 12a^2-6ab+9)=2a^2+4ab+3-\frac 12a^2-6ab+9$　　

$=\frac 32a^2-2ab+12 .$　　

故丙的代数是为$\frac 32a^2-2ab+12 .$