《2025年同步练习江苏七年级数学上册苏科版》

12. 用简便方法计算：某种粮专业户出售余粮10袋,每袋质量如下(单位：kg).
199,201,197,203,200,195,197,199,202,196.
(1)以每袋余粮200 kg为标准,求这10袋余粮总计超过(或不足)多少千克.
(2)这10袋余粮一共多少千克?

答案：
(1)-1+1-3+3+0-5-3-1+2-4=-11,所以不足11 kg
(2)10×200-11=1 989(kg),一共1 989 kg

13. 在如图的数轴上先画出位于点A右边4个单位长度的点B,在原点左边画点C,使B,C两点到原点的距离相等,写出B,C两点所表示的数,并求A,C两点间的距离.

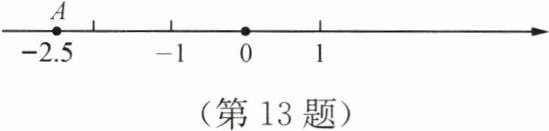
答案： 点B表示1.5 点C表示-1.5 AC=1

14. 已知$m＞0$,$n＜0$,$|n|＞|m|$,请你结合数轴,用“＜”连接$m$,$n$,$-m$,$-n$.

答案： n＜-m＜m＜-n

15. 阅读下列材料：对于有理数x,$|x|= \begin{cases} x, & x＞0, \\ 0, & x= 0, \\ -x, & x＜0. \end{cases} $可知,当$x＜0$时,$\frac{x}{|x|}= \frac{x}{-x}= -1$.
用这个结论解答问题：
(1)已知a,b是有理数,当$ab＞0$时,求$\frac{a}{|a|}+\frac{b}{|b|}$的值；
(2)已知a,b,c是有理数,当$abc＞0$时,求$\frac{a}{|a|}+\frac{b}{|b|}+\frac{c}{|c|}$的值；
(3)已知a,b,c是有理数,$a+b+c= 0$,$abc＜0$,求$\frac{b+c}{|a|}+\frac{a+c}{|b|}+\frac{a+b}{|c|}$的值.

答案：

解：$(1)$当$ab＞0$时，则$a＞0，$$b＞0$或$a＜0，$$b＜0.$　　

当$a＞0，$$b＞0$时，$\frac {a}{|a|}+\frac b{|b|}=1+1=2.$　　

当$a＜0，$$b＜0$时，$\frac {a}{|a|}+\frac b{|b|}=-1+(-1)=-2.$　　

故$\frac {a}{|a|}+\frac b{|b|}$的值为$±2.$　　

$(2)$当$abc＞0$时，则$a，$$b，$$c $为三正或两负一正$.$　　

当$a，$$b，$$c $都为正数时，$\frac {a}{|a|}+\frac b{|b|}+\frac c{|c|}=1+1+1=3.$　　

当$a，$$b，$$c $为两负一正时，$\frac {a}{|a|}+\frac b{|b|}+\frac c{|c|}=(-1)+(-1)+1=-1.$　　

故$\frac {a}{|a|}+\frac b{|b|}+\frac c{|c|}$的值为$3$或$-1.$　　

$(3)$因为$a+b+c=0，$　　

所以$a+b=-c，$$b+c=-a，$$a+c=-b.$　　

当$abc＜0$时，则$a，$$b，$$c $为三负或两正一负$.$　　

当$a，$$b，$$c $为三负时，$a+b+c=0$不成立，舍　　

当$a，$$b，$$c $为两正一负时，$\frac {b+c}{|a|}+\frac {a+c}{|b|}+\frac {a+b}{|c|}=\frac {-a}{|a|}+\frac {-b}{|b|}+\frac {-c}{|c|}=(-1)+(-1)+1=-1 .$　　

故$\frac {b+c}{|a|}+\frac {a+c}{|b|}+\frac {a+b}{|c|}$的值为$-1.$