第73页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
1. 填空题。
(1)一个梯形的上底是6 m,下底是10 m,高是2.5 m,这个梯形的面积是( )$m^{2}$。
(2)一个梯形的面积是$68.4cm^{2}$,上、下底之和是36 cm,这个梯形的高是( )cm。
(3)一个直角梯形的上底、下底和高分别是10 dm、12 dm 和8 dm,它的面积是( )$dm^{2}$。
在梯形内画一个最大的正方形,正方形的面积是( )$dm^{2}$。
(1)一个梯形的上底是6 m,下底是10 m,高是2.5 m,这个梯形的面积是( )$m^{2}$。
(2)一个梯形的面积是$68.4cm^{2}$,上、下底之和是36 cm,这个梯形的高是( )cm。
(3)一个直角梯形的上底、下底和高分别是10 dm、12 dm 和8 dm,它的面积是( )$dm^{2}$。
在梯形内画一个最大的正方形,正方形的面积是( )$dm^{2}$。
答案:
1.
(1)20
(2)3.8
(3)88 64
解析
(1)$S=(a+b)×h÷2$。
(2)$h=S×2÷(a+b)$。
(3)$S=(a+b)×h÷2$。$S=a^{2}$,a最大为直角梯形的高。
(1)20
(2)3.8
(3)88 64
解析
(1)$S=(a+b)×h÷2$。
(2)$h=S×2÷(a+b)$。
(3)$S=(a+b)×h÷2$。$S=a^{2}$,a最大为直角梯形的高。
2. 选择题。(将正确答案的序号填在括号里)
(1)如图,将一个梯形分成三部分,这三部分面积的大小关系正确的是( )。
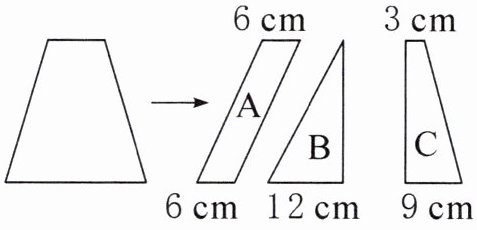
A.A部分的面积最大 B.B部分的面积最大
C.C部分的面积最大 D.三个部分面积一样大
(2)把两个完全一样的直角三角形拼起来,不可能得到的图形是( )。
A.正方形 B.平行四边形 C.三角形 D.梯形
(1)如图,将一个梯形分成三部分,这三部分面积的大小关系正确的是( )。

A.A部分的面积最大 B.B部分的面积最大
C.C部分的面积最大 D.三个部分面积一样大
(2)把两个完全一样的直角三角形拼起来,不可能得到的图形是( )。
A.正方形 B.平行四边形 C.三角形 D.梯形
答案:
2.
(1)D
(2)D
解析
(1)假设梯形的高为h。A部分:$6×h=6h$。B部分:$12×h÷2=6h$。C部分:$(3+9)×h ÷2=6h$,所以A、B、C三部分面积相等。本题选D。
(2)根据图形拼一拼可以得出结论。本题选D。
(1)D
(2)D
解析
(1)假设梯形的高为h。A部分:$6×h=6h$。B部分:$12×h÷2=6h$。C部分:$(3+9)×h ÷2=6h$,所以A、B、C三部分面积相等。本题选D。
(2)根据图形拼一拼可以得出结论。本题选D。
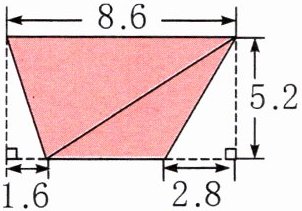
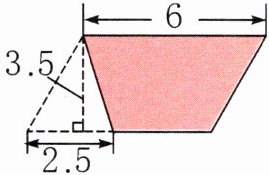
3. 求下列图形涂色部分的面积。(单位:cm)


答案:
3.第一个:$a=8.6−1.6−2.8=4.2(cm)$
$S=(a+b)×h÷2=(4.2+8.6)×5.2÷2 =33.28(cm^{2})$
第二个:$a=6−2.5=3.5(cm)$
$S=(a+b)×h÷2=(3.5+6)×3.5÷2 =16.625(cm^{2})$
解析:平行四边形的对边相等,寻找梯形的上底、下底和高,再根据梯形面积公式计算即可。
$S=(a+b)×h÷2=(4.2+8.6)×5.2÷2 =33.28(cm^{2})$
第二个:$a=6−2.5=3.5(cm)$
$S=(a+b)×h÷2=(3.5+6)×3.5÷2 =16.625(cm^{2})$
解析:平行四边形的对边相等,寻找梯形的上底、下底和高,再根据梯形面积公式计算即可。
4. 如图,每小格的边长为1 cm,先算一算,再画一画、填一填。

(1)图中梯形的面积是( )$cm^{2}$。
(2)在图中画一个和梯形面积相等的平行四边形。
(3)再画一个面积为梯形面积一半的三角形,要求三角形的底是3 cm,它的高是( )cm。

(1)图中梯形的面积是( )$cm^{2}$。
(2)在图中画一个和梯形面积相等的平行四边形。
(3)再画一个面积为梯形面积一半的三角形,要求三角形的底是3 cm,它的高是( )cm。
答案:
4.
(1)12
(2)

(3)见第2题图 4 (画法不唯一)
解析
(1)梯形面积$=S=(a+b)×h÷2$。
(2)平行四边形面积$=S=ah$,画一个与
(1)中面积相等的平行四边形,即$ah=12(cm^{2})$即可。
(3)三角形面积$=S=ah÷2$,画一个面积为梯形面积一半的三角形,即$S=ah÷2=12÷2$,那么$ah=12(cm^{2})$。三角形高=三角形面积×2÷底,即$12÷2×2÷3=4$。
4.
(1)12
(2)

(3)见第2题图 4 (画法不唯一)
解析
(1)梯形面积$=S=(a+b)×h÷2$。
(2)平行四边形面积$=S=ah$,画一个与
(1)中面积相等的平行四边形,即$ah=12(cm^{2})$即可。
(3)三角形面积$=S=ah÷2$,画一个面积为梯形面积一半的三角形,即$S=ah÷2=12÷2$,那么$ah=12(cm^{2})$。三角形高=三角形面积×2÷底,即$12÷2×2÷3=4$。
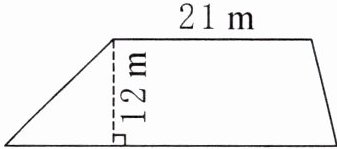
5. 在国庆节期间,市中心广场东面布置了一个大型的梯形花卉盆景(如下图),它的上底是21 m,高是12 m,整个盆景占地面积是$336m^{2}$。这个梯形的下底是多少米?(列方程解答)

答案:
5.解:设这个梯形的下底是x米。
$(21+x)×12÷2=336$
$x=35$
解析:根据“(上底+下底)×高÷2=梯形面积”列方程求解即可。
$(21+x)×12÷2=336$
$x=35$
解析:根据“(上底+下底)×高÷2=梯形面积”列方程求解即可。
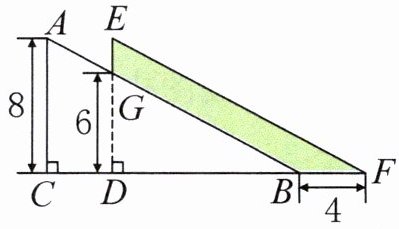
6. [拓展题]小书将两个完全相同的直角三角形的一部分叠放在一起(如下图),涂色部分的面积是多少平方厘米?(单位:cm)

答案:
6.因为三角形ABC和三角形EFD面积相等,所以梯形ACDG和梯形BGEF(即涂色部分)面积相等。
$(6+8)×4÷2=28(cm^{2})$
解析:已知三角形ABC和三角形EFD是两个完全相同的直角三角形,它们同时减去三角形GDB,剩下的梯形ACDG和梯形BGEF的面积是相等的,再用梯形的面积公式计算即可。
$(6+8)×4÷2=28(cm^{2})$
解析:已知三角形ABC和三角形EFD是两个完全相同的直角三角形,它们同时减去三角形GDB,剩下的梯形ACDG和梯形BGEF的面积是相等的,再用梯形的面积公式计算即可。
查看更多完整答案,请扫码查看


