《2025年名师面对面先学后练五年级数学上册人教版》

1.填空题。
(1)一个三角形和一个平行四边形的底和面积分别相等,平行四边形的高是10 cm,三角形的高是( )cm。
(2)一个三角形的面积比与它等底等高的平行四边形的面积少$32.5dm^2,$这个平行四边形的面积是$( )dm^2,$三角形的面积是$( )dm^2。$
(3)一个等边三角形的周长是24.6 dm,某条底上的高是7.1 dm,这个等边三角形的面积是$( )dm^2,$与它等底等高的平行四边形的面积是$( )dm^2。$
(4)一块长方形红绸的长是2.4 m,宽是7 dm,要做成如右图所示的三角形小旗,可以做( )面。

答案： 1.
(1)20
(2)65 32.5
(3)29.11 58.22
(4)840 解析
(1)三角形面积=底×高÷2,平行四边形面积=底×高,底和面积都相等,说明三角形的高÷2=平行四边形的高,所以三角形的高=平行四边形的高×2。
(2)三角形的面积是与它等底等高的平行四边形的面积的一半,少32.5dm²就是少一半的面积,即三角形的面积是32.5dm²,那么平行四边形的面积=三角形的面积×2=32.5×2=65(dm²)。
(3)等边三角形的周长是24.6dm,那么这个三角形的边长=24.6÷3=8.2(dm),由“S=ah÷2”可知,等边三角形的面积=8.2×7.1÷2=29.11(dm²),平行四边形的面积=8.2×7.1=58.22(dm²)。
(4)先换算单位,再计算长方形红绸的长和宽最大能容纳几面三角形小旗的长和宽,分别相除,求出长方形红绸最多能做2×30×14=840(面)三角形小旗。

2.选择题。(将正确答案的序号填在括号里)
(1)如图,三角形面积等于左边平行四边形面积一半的是( ),三角形面积等于左边平行四边形面积的是( )。
A.①
B.②
C.③
D.④

(2)如图,平行四边形的面积是$138cm^2,$它的底被平均分成了3等份,涂色部分的面积是$( )cm^2。$
A.69
B.34.5
C.23
D.无法确定

答案： 2.
(1)A C
(2)C 解析
(1)左边平行四边形的面积=4×3=12。①的面积=4×3÷2=6,面积是左边平行四边形的面积的一半。②的面积=3×3÷2=4.5。③的面积=4×6÷2=12,面积等于左边平行四边形的面积。④的面积=3×3÷2=4.5。
(2)把平行四边形分为2个大三角形,大三角形面积是涂色部分面积的3倍,可得平行四边形面积是涂色部分面积的2×3=6倍,那么涂色部分面积=138÷6=23(cm²)。本题选C。

3.如图,哪几对三角形的面积相等(两条虚线互相平行)?你还能画出几个和三角形MNG面积相等的三角形?

我发现：等底等高的两个三角形面积( )。

答案： 3. 三角形NMG和三角形NHG面积相等,三角形NMO和三角形GHO面积相等,三角形NMH和三角形GHM面积相等。 相等 还能画出无数个和三角形MNG面积相等的三角形。 解析 本题主要寻找三角形的底和高,底和高都相等的三角形面积相等。满足底和高与三角形MNG底和高相等的三角形有很多个。

4.一个三角形的底长6 m。如果底延长2 m,那么面积就增加$3m^2。$原来三角形的面积是多少平方米?

答案： 4.3×2÷2=3(m) 6×3÷2=9(m²) 解析 空白部分的三角形和涂色部分三角形的高相同。先根据“h=S×2÷a”,求出三角形的高,再根据“S=ah÷2”,求出空白部分的面积。

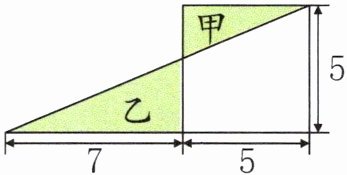
5.【拓展题】如图,涂色部分甲比乙的面积小多少?(单位:cm)

答案： 5.(5+7)×5÷2-5×5=5(cm²) 解析 两个涂色部分分别加上空白部分的面积就是大三角形和正方形各自的面积,求甲的面积比乙的面积小多少,相当于求正方形面积比大三角形面积小多少,求出大三角形和正方形的面积再相减即可。