第45页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
1. 填空题。
(1)根据运算律在□里填上适当的数或字母。
x+(7+y)= (□+□)+□
2y+3y= (□+□)·□
a·b·9= □·(□·□)
(a+5)×15= □×□+□×□
(2)用字母表示出长方形和正方形的周长和面积。

C= ______
S= ______
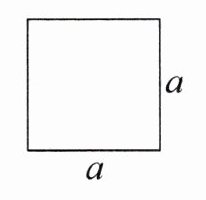
C= ______
S= ______
(3)用s表示路程,v表示速度,t表示时间。
①s= ( ),v= ( ),t= ( )。
②如果每分钟行驶65 m,行驶了10分钟,那么路程是( )m。
(1)根据运算律在□里填上适当的数或字母。
x+(7+y)= (□+□)+□
2y+3y= (□+□)·□
a·b·9= □·(□·□)
(a+5)×15= □×□+□×□
(2)用字母表示出长方形和正方形的周长和面积。

C= ______
S= ______

C= ______
S= ______
(3)用s表示路程,v表示速度,t表示时间。
①s= ( ),v= ( ),t= ( )。
②如果每分钟行驶65 m,行驶了10分钟,那么路程是( )m。
答案:
1.
(1)x 7 y 2 3 y a b 9
a 15 5 15
(2)2(a+b) ab 4a a²
(3)①vt s÷t s÷v ②650
解析
(1)考查加法结合律、乘法分配律、乘法结合律以及用字母表示数。
(2)长方形周长=(长+宽)×2,长方形面积=长×宽,正方形周长=边长×4,正方形面积=边长×边长,用字母表示长方形、正方形的周长及面积公式。
(3)①路程=速度×时间,速度=路程÷时间,时间=路程÷速度。注意省略乘号。
②s=vt,v=65,t=10,代入算值即可。
(1)x 7 y 2 3 y a b 9
a 15 5 15
(2)2(a+b) ab 4a a²
(3)①vt s÷t s÷v ②650
解析
(1)考查加法结合律、乘法分配律、乘法结合律以及用字母表示数。
(2)长方形周长=(长+宽)×2,长方形面积=长×宽,正方形周长=边长×4,正方形面积=边长×边长,用字母表示长方形、正方形的周长及面积公式。
(3)①路程=速度×时间,速度=路程÷时间,时间=路程÷速度。注意省略乘号。
②s=vt,v=65,t=10,代入算值即可。
2. 判断题。(对的画“√”,错的画“×”)
(1)无论a取什么值$,2a= a^2。$( )
$(2)m^2$表示2个m相乘,2m表示2个m相加。( )
(3)根据乘法分配律$,2x+x^2$可以写成x(2+x)。( )
(4)(x+y)×2可以写成2(x+y)。( )
(1)无论a取什么值$,2a= a^2。$( )
$(2)m^2$表示2个m相乘,2m表示2个m相加。( )
(3)根据乘法分配律$,2x+x^2$可以写成x(2+x)。( )
(4)(x+y)×2可以写成2(x+y)。( )
答案:
2.
(1)×
(2)√
(3)√
(4)√
解析
(1)举例子,a=1,2a=2,a²=1,不相等;a =0,a=2时,2a=a²。本题说法错误。
(2)考查m²和2m的区别。本题说法正确。
(3)x²=x·x,2x+x²=2x+x·x=x(2+x)。本题说法正确。
(4)省略乘号时,一般把数写在字母前面。本题说法正确。
(1)×
(2)√
(3)√
(4)√
解析
(1)举例子,a=1,2a=2,a²=1,不相等;a =0,a=2时,2a=a²。本题说法错误。
(2)考查m²和2m的区别。本题说法正确。
(3)x²=x·x,2x+x²=2x+x·x=x(2+x)。本题说法正确。
(4)省略乘号时,一般把数写在字母前面。本题说法正确。
3. 连线题。
(1)把结果相等的两个式子连起来。

(2)把问题和相应的式子用线连起来。
椅子的单价是a元,课桌的单价是椅子的1.2倍。
一套桌椅多少元? 1.2a
300元可以买多少把椅子? a+1.2a
课桌的单价比椅子多多少元? 300÷a
课桌的单价是多少元? 1.2a-a
(1)把结果相等的两个式子连起来。

(2)把问题和相应的式子用线连起来。
椅子的单价是a元,课桌的单价是椅子的1.2倍。
一套桌椅多少元? 1.2a
300元可以买多少把椅子? a+1.2a
课桌的单价比椅子多多少元? 300÷a
课桌的单价是多少元? 1.2a-a
答案:
3.
(1)

(2)

解析
(1)省略乘号时,一般把数写在字母前面。x·x=x²,表示2个x相乘,读作x的平方。
(2)“课桌的单价是椅子的1.2倍”,是把椅子的单价看作标准量。课桌单价=椅子单价×1.2,即1.2a。一套桌椅的价格=课桌单价+椅子单价,即1.2a+a。求300元可以买多少把椅子,相当于求300里有多少个a,即300÷a。求课桌的单价比椅子多多少元,即1.2a-a。
3.
(1)

(2)

解析
(1)省略乘号时,一般把数写在字母前面。x·x=x²,表示2个x相乘,读作x的平方。
(2)“课桌的单价是椅子的1.2倍”,是把椅子的单价看作标准量。课桌单价=椅子单价×1.2,即1.2a。一套桌椅的价格=课桌单价+椅子单价,即1.2a+a。求300元可以买多少把椅子,相当于求300里有多少个a,即300÷a。求课桌的单价比椅子多多少元,即1.2a-a。
4. 如图,空白部分是一个正方形。你能用字母表示出空白部分和涂色部分的面积吗?


答案:
4. 空白部分:S=m² 涂色部分:S=mn-m²
解析 长方形面积=长×宽=mn,正方形边长等于长方形的宽,所以正方形面积=边长×边长=m²。因此涂色部分的面积=长方形面积-正方形面积=mn-m²。
解析 长方形面积=长×宽=mn,正方形边长等于长方形的宽,所以正方形面积=边长×边长=m²。因此涂色部分的面积=长方形面积-正方形面积=mn-m²。
查看更多完整答案,请扫码查看


