《2025年通成学典课时作业本九年级数学上册人教版浙江专版》

11. (2023·温岭一模)将等腰直角三角尺与量角器按如图所示的方式摆放,使三角尺的直角顶点与量角器的中心O重合,三角尺内部的小等腰直角三角形的两个顶点A,B恰好落在量角器的边缘,对应的刻度分别是70°,130°. 若AC= 5,则$\overset{\frown}{AB}$与AB所围图形的面积为______.

答案： $\frac{50π−75\sqrt{3}}{6}$　解析:如图,连接OA,OB,过点A作AD⊥OB 于点D.
∵$△ABC$是等腰直角三角形,$AC=5$,
∴由勾股定理,易得$AB=5\sqrt{2}$.
∵点A,B对应的刻度分别是$70^{\circ },130^{\circ }$,
∴$∠AOB=130^{\circ }-70^{\circ }=60^{\circ }$.
∵$OA=OB$,
∴$△AOB$是等边三角形.
∴$OA=OB=AB=5\sqrt{2},∠ABO=60^{\circ }$,则$∠BAD=30^{\circ }$.
∴$BD=\frac {1}{2}AB=\frac {5\sqrt{2}}{2}$,则$AD=\sqrt {AB^{2}-BD^{2}}=\frac {5\sqrt{6}}{2}$.
∴所求面积为$S_{扇形AOB}-S_{△AOB}=\frac {60π×(5\sqrt{2})^{2}}{360}-\frac {1}{2}×5\sqrt{2}×\frac {5\sqrt{6}}{2}=\frac{50π−75\sqrt{3}}{6}$

12. 已知⊙O的半径为5,弦AB= 8,M是AB上一点,且OM的长为整数,则点M不同的位置有 ( )

A.6个
B.5个
C.4个
D.3个

答案： B

13. 若点O是等腰三角形ABC的外心,且∠BOC= 60°,底边BC= 2,则△ABC的面积为 ( )

A.$2 + \sqrt{3}$
B.$\frac{2\sqrt{3}}{3}$
C.$2 + \sqrt{3}或2 - \sqrt{3}$
D.$4 + 2\sqrt{3}或2 - \sqrt{3}$

答案： C

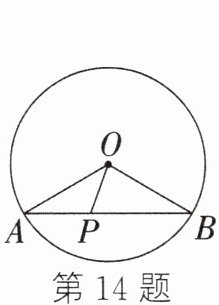
14. 如图,⊙O的半径是2,AB是⊙O的弦,P是弦AB上的动点,且1≤OP≤2,则弦AB所对的圆周角的度数为 ( )

A.60°
B.120°
C.60°或120°
D.30°或150°

答案： C

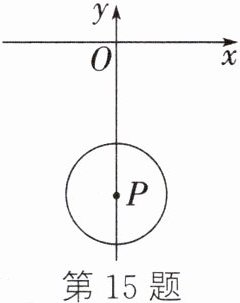
15. 如图,在平面直角坐标系中,点P的坐标为(0,-6),⊙P的半径为2,⊙P沿y轴以2个单位长度/秒的速度向正方向运动,则当⊙P与x轴相切时,⊙P运动的时间为 ( )

A.2秒
B.3秒
C.2秒或4秒
D.3秒或4秒

答案： C

16. 在半径为25cm的⊙O中,弦AB= 40cm,则弦AB所对的弧的中点到该弦的距离为______.

答案： 10cm或40cm

17. 已知⊙O的半径为2,弦BC= $2\sqrt{3}$,A是⊙O上一点,且AB= AC,直线OA与BC交于点D,则AD的长为______.

答案： 3或1

18. 已知AB是⊙O的直径,半径OC⊥AB,点D在⊙O上,且点D与点C在直径AB的两侧,连接CD,BD. 若∠OCD= 22°,则∠ABD的度数为______.

答案： $23^{\circ }$或$67^{\circ }$

19. 在Rt△ABC中,∠C= 90°,AC= 6,BC= 8,以点C为圆心,r为半径作圆,⊙C与斜边AB只有一个公共点. 求半径r的取值范围.

答案： 在$Rt△ABC$中,由勾股定理,得$AB=\sqrt {BC^{2}+AC^{2}}=\sqrt {8^{2}+6^{2}}=10$.
∵易得斜边上的高为$\frac {8×6}{10}=\frac {24}{5}$,
∴当圆和斜边相切时,$r=\frac {24}{5}$;当圆和斜边相交,且只有一个交点时,$6＜r≤8$.综上所述，半径r的取值范围是$r=\frac {24}{5}$或$6＜r≤8$