《2025年通成学典课时作业本九年级数学上册人教版浙江专版》

1. 把一个平面图形绕着平面内某一点O______,叫做图形的旋转,点O叫做______,转动的角叫做______.
2. 如果图形上的点P经过旋转变为点P',那么这两个点叫做这个旋转的______.
3. 旋转的性质：对应点到旋转中心的距离______；对应点与旋转中心所连线段的夹角等于______；旋转前、后的图形______.
4. 图形的旋转由______、______、______所决定.

答案： 1. 转动一个角度 旋转中心 旋转角 2. 对应点 3. 相等 旋转角 全等 4. 旋转中心 旋转角度 旋转方向

1. 下列现象中,属于旋转的是( )

A.摩托车在急刹车时向前滑动
B.电梯的上下运动
C.拧开水龙头的过程
D.飞机起飞后冲向空中的过程

答案： C

2. (2023·天津)如图,将△ABC绕点A按逆时针方向旋转得到△ADE,点B,C的对应点分别是D,E,且点E在BC的延长线上,连接BD,则下列结论中,一定正确的是( )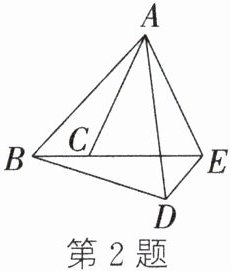

A.∠CAE= ∠BED
B.AB= AE
C.∠ACE= ∠ADE
D.CE= BD

答案： A

3. (2023·温岭期中)如图,在Rt△ABC中,∠CAB= 90°,∠B= 60°,$AC= 2\sqrt{3}$. 将Rt△ABC绕点A按顺时针方向旋转一定角度得到Rt△ADE. 若点B的对应点D恰好落在边BC上,则CD的长为( )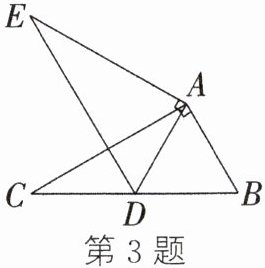

A.1
B.$\sqrt{3}$
C.2
D.$4-\sqrt{3}$

答案： C

4. (2023·张家界)如图,AO为∠BAC的平分线,且∠BAC= 50°,将四边形ABOC绕点A按逆时针方向旋转后,得到四边形AB'O'C',且∠OAC'= 100°,则四边形ABOC旋转的角度是______.

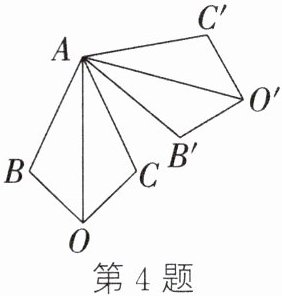
答案： 75°

5. 如图,在Rt△ABC中,∠C= 90°,∠ABC= 30°,AC= 1 cm,将Rt△ABC绕点A按逆时针方向旋转得到Rt△AB'C',使得点C'落在边AB上,连接BB',则BB'的长是______.

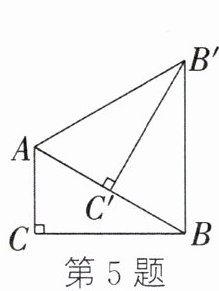
答案： 2 cm

6. 如图,将一把直角三角尺ABC绕30°角的顶点B按顺时针方向旋转,使得点A与CB的延长线上的点E重合.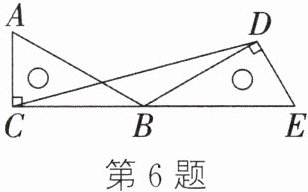
(1)直角三角尺最少旋转了多少度？
(2)连接CD,求∠BDC的度数.

答案： （1）∠ABE=180°-30°=150°，即直角三角尺最少旋转了150° （2）由旋转的性质，知BC=BD，∠DBE=∠ABC=30°，
∴易得∠BDC=$\frac{1}{2}×30^{\circ}=15^{\circ}$