《2025年通成学典课时作业本九年级数学上册人教版浙江专版》

1. 下列说法中,错误的是 ( )

A.长度相等的两条弧是等弧
B.直径是圆中最长的弦
C.面积相等的两个圆是等圆
D.半径相等的两个半圆是等弧

答案： A

2. 下列说法中,正确的是 ( )

A.相等的圆心角所对的弧相等
B.相等的弦所对的弧相等
C.相等的圆周角所对的弧相等
D.相等的弧所对的弦相等

答案： D

3. 有下列结论：① 垂直于半径的直线是圆的切线；② 平分弦的直径垂直于弦；③ 三角形有且只有一个外接圆. 其中,正确的有 ( )

A.0个
B.1个
C.2个
D.3个

答案： B

4. 如图,每个小三角形都是边长相等的正三角形,则△ABC 的外心是 ( )

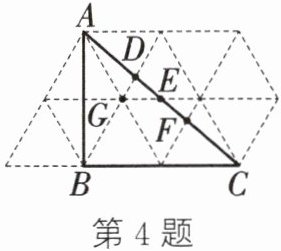
A.点D
B.点E
C.点F
D.点G

答案： B

5. 如图,在四边形ABCD中,AB= AD= 5,BC= CD,且BC＞AB,BD= 8. 当A,B,C,D四点在同一个圆上时,求该圆的半径.

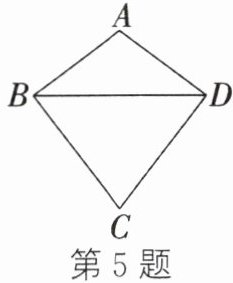
答案： 连接AC.
∵A,B,C,D四点在同一个圆上,
∴可设此圆为$\odot O$,并作出$\odot O$,且四边形ABCD为$\odot O$的内接四边形.
∵$AB=AD,BC=CD$,
∴AC垂直平分线段BD,$\widehat {AB}=\widehat {AD}$,$\widehat {BC}=\widehat {CD}$,
∴$\widehat {AB}+\widehat {BC}=\widehat {AD}+\widehat {CD}$.
∴易知AC是$\odot O$的直径,即圆心O是AC的中点.设$AC⊥BD$于点E,连接OB.
∵$AC⊥$BD,
∴$BE=\frac {1}{2}BD=4$.又
∵$AB=5$,
∴$AE=\sqrt {AB^{2}-BE^{2}}=3$.设$OE=x$,则$OB=OA=3+x$.在$Rt△BEO$中,
∵$OB^{2}=BE^{2}+OE^{2}$,
∴$(3+x)^{2}=4^{2}+x^{2}$,解得$x=\frac {7}{6}$.
∴该圆的半径为$\frac {7}{6}+3=\frac {25}{6}$

6. 已知⊙O的直径为6cm,点A不在⊙O内,则OA的长 ( )

A.大于3cm
B.不小于3cm
C.大于6cm
D.不小于6cm

答案： B

7. 若⊙O的半径为4,点O到直线m的距离为3,则直线m与⊙O的公共点的个数为 ( )

A.0
B.1
C.2
D.3

答案： C

8. 已知⊙A的半径为5,圆心A的坐标为(1,0),点P的坐标为(-2,4),则点P与⊙A的位置关系是 ( )

A.点P在⊙A上
B.点P在⊙A内
C.点P在⊙A外
D.无法确定

答案： A

9. 以坐标原点O为圆心,作半径为3的圆. 若直线y= x-b与⊙O相交,求b的取值范围.______

答案： 如图,当直线$y=x-b$经过第一、二、三象限时,与$\odot O$相切于点C,与x轴、y轴交于点B,A,连接OC.
∴$OC⊥AB$.在$y=x-b$中,令$x=0$,则$y=-b$,
∴点A的坐标为$(0,-b)$.令$y=0$,则$x=b$,
∴点B的坐标为$(b,0)$.
∴易知$OA=OB$,即$△OAB$是等腰直角三角形.
∵$OC⊥AB,OC=3$,
∴易知$AC=OC=3$.
∴$OA=\sqrt {AC^{2}+OC^{2}}=3\sqrt {2}$.
∴$b=-3\sqrt {2}$.同理，可知当直线$y=x-b$经过第一、三、四象限时,与$\odot O$相切于点D,连接OD.此时易知直线$y=x-b$与y轴的交点坐标为$(0,-3\sqrt {2})$.
∴$b=3\sqrt {2}$.
∴当直线$y=x-b$与$\odot O$相交时,b的取值范围是$-3\sqrt {2}＜b＜3\sqrt {2}$

10. (2022·台州)一个垃圾填埋场,它在地面上的形状为长80m、宽60m的矩形,有污水从该矩形的四周边界向外渗了3m,则该垃圾填埋场外围受污染土地的面积为 ( )

A.$(840 + 6\pi)\ m^2$
B.$(840 + 9\pi)\ m^2$
C.$840\ m^2$
D.$876\ m^2$

答案： B