《2025年通成学典课时作业本九年级数学上册人教版浙江专版》

1. 到圆心的距离等于圆的______的直线是圆的切线.
2. 经过半径的外端并且______这条半径的直线是圆的切线.
3. 圆的切线垂直于______的半径.

答案： 1. 半径 2. 垂直于 3. 过切点

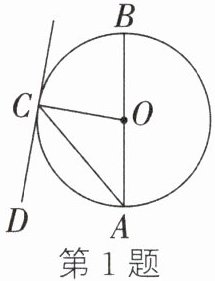
1. (2023·重庆B卷)如图,AB为⊙O的直径,直线CD与⊙O相切于点C,连接AC,OC.若$\angle ACD= 50^\circ,则\angle BAC的度数为( )A. 30^\circB. 40^\circC. 50^\circD. 60^\circ$
]

答案： B

2. 如图,AB是⊙O的直径,BC交⊙O于点D,DE⊥AC于点E,连接OD.若要使DE是⊙O的切线,还需补充一个条件,则下列补充的条件中,不正确的是( )

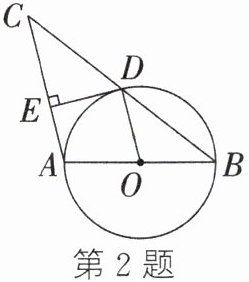
A.DE= OD
B.AB= AC
C.CD= BD
D.AC// OD
]

答案： A

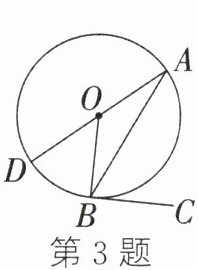
3. (2023·邵阳)如图,AD是⊙O的直径,AB是⊙O的弦,BC与⊙O相切于点B,连接OB.若$\angle ABC= 65^\circ,则\angle BOD$的度数为______.
]

答案： 50°

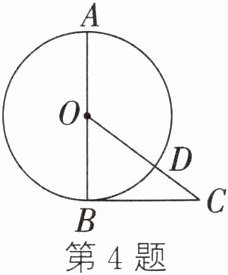
4. 如图,AB是⊙O的直径,点O是圆心,BC与⊙O相切于点B,OC交⊙O于点D,且BC= 8,CD= 4,则⊙O的半径是______.
]

答案： 6

5. (2022·椒江期末)如图,在△ABC中,AB= AC,$\angle BAC= 120^\circ,$⊙O经过点A和点B且与边BC相交于点D.
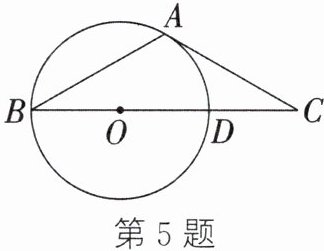
(1)试判断AC与⊙O的位置关系,并说明理由；
(2)当CD= 5时,求⊙O的半径.
]

答案：
（1）AC是⊙O的切线 理由:如图,连接OA.
∵AB=AC，∠BAC=120°，
∴∠B=∠C=$\frac{1}{2}$（180°-∠BAC）=30°.
∵OA=OB，
∴∠BAO=∠B=30°.
∴∠OAC=∠BAC-∠BAO=120°-30°=90°.
∴OA⊥AC.
∵OA是⊙O的半径，
∴AC是⊙O的切线. （2）如图,连接AD.
∵OA=OD，∠AOD=∠B+∠BAO=60°，
∴△AOD是等边三角形.
∴AD=OD，∠ADO=60°.
∴∠CAD=∠ADO-∠C=30°.
∴∠CAD=∠C=30°.
∴AD=CD=OD=5.
∴⊙O的半径为5

6. 如图,AB是⊙O的直径,C为⊙O上一点,过点C的切线与AB的延长线交于点P.若$AC= PC= 3\sqrt{3},$则PB的长为$( )A. \sqrt{3}B. \frac{3}{2}C. 2\sqrt{3}D. 3$
]

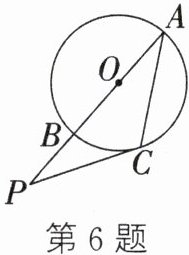
答案： D