9. (2023·台州)已知抛物线$y= ax^{2}-a(a≠0)与直线y= kx交于A(x_{1},y_{1}),B(x_{2},y_{2})$两点.若$x_{1}+x_{2}<0$,则直线$y= ax+k$一定经过( )
A.第一、二象限
B.第二、三象限
C.第三、四象限
D.第一、四象限
A.第一、二象限
B.第二、三象限
C.第三、四象限
D.第一、四象限
答案:
D
10. 已知二次函数$y= -\frac{1}{3}x^{2}+2$,则当$1≤x≤5$时,$y$的最大值为( )
A.2
B.$\frac{2}{3}$
C.$\frac{5}{3}$
D.$\frac{7}{3}$
A.2
B.$\frac{2}{3}$
C.$\frac{5}{3}$
D.$\frac{7}{3}$
答案:
C
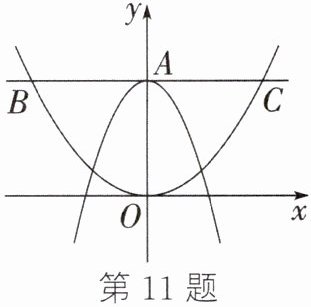
11. 如图,在平面直角坐标系中,抛物线$y= ax^{2}+4与y轴交于点A$,过点$A与x轴平行的直线交抛物线y= \frac{1}{4}x^{2}于点B,C$,则$BC$的长为______.

答案:
8
12. 已知二次函数$y= -x^{2}+2(m-1)x+2m-m^{2}的图象关于y$轴对称,则由此图象的顶点$A和图象与x轴的两个交点B,C$(点$B在点C$的右侧)构成的$\triangle ABC$的面积是______.
答案:
1 解析:
∵二次函数$y=-x^{2}+2(m-1)x+2m-m^{2}$的图象关于y轴对称,
∴易知$2(m-1)=0$,解得$m=1$.
∴$y=-x^{2}+1$.
∴易得顶点A的坐标为$(0,1)$,图象与x轴的两个交点B,C的坐标分别为$(1,0),(-1,0)$.
∴$\triangle ABC$的面积为$\frac {1}{2}×[1-(-1)]×1=1.$
∵二次函数$y=-x^{2}+2(m-1)x+2m-m^{2}$的图象关于y轴对称,
∴易知$2(m-1)=0$,解得$m=1$.
∴$y=-x^{2}+1$.
∴易得顶点A的坐标为$(0,1)$,图象与x轴的两个交点B,C的坐标分别为$(1,0),(-1,0)$.
∴$\triangle ABC$的面积为$\frac {1}{2}×[1-(-1)]×1=1.$
13. 已知抛物线$y= ax^{2}+k的顶点坐标是(0,-2)$,且过点$(1,1)$.
(1) 求此抛物线对应的函数解析式,并指出此抛物线的开口方向及对称轴.
(2) 此抛物线对应的函数$y$有最大值还是最小值?其值是多少?
(3) 若$M(x_{1},y_{1}),N(x_{2},y_{2})$是抛物线上的两点,且$x_{1}<x_{2}<0$,则$y_{1}与y_{2}$的大小关系如何?
(1) 求此抛物线对应的函数解析式,并指出此抛物线的开口方向及对称轴.
(2) 此抛物线对应的函数$y$有最大值还是最小值?其值是多少?
(3) 若$M(x_{1},y_{1}),N(x_{2},y_{2})$是抛物线上的两点,且$x_{1}<x_{2}<0$,则$y_{1}与y_{2}$的大小关系如何?
答案:
(1)由题意,得$\begin{cases}k = - 2\\a + k = 1\end{cases}$,解得$\begin{cases}a = 3\\k = - 2\end{cases}$,
∴此抛物线对应的函数解析式为$y = 3x^{2}-2$,抛物线的开口向上,对称轴为y轴.(2)此抛物线对应的函数y有最小值,当$x = 0$时,函数y取得最小值,为$-2$.(3)当$x<0$时,y随x的增大而减小.
∵$x_1<x_2<0$,
∴$y_1>y_2$.
∴此抛物线对应的函数解析式为$y = 3x^{2}-2$,抛物线的开口向上,对称轴为y轴.(2)此抛物线对应的函数y有最小值,当$x = 0$时,函数y取得最小值,为$-2$.(3)当$x<0$时,y随x的增大而减小.
∵$x_1<x_2<0$,
∴$y_1>y_2$.
14. 如图,抛物线$y= ax^{2}+4与x轴交于A,B$两点(点$A在点B$的左侧),与$y轴交于点C$,且$AB= 4$.
(1) 求抛物线对应的函数解析式;
(2) 若点$P$在第一象限的抛物线上,且$\angle CAP= 45^{\circ}$,求点$P$的坐标.

(1) 求抛物线对应的函数解析式;
(2) 若点$P$在第一象限的抛物线上,且$\angle CAP= 45^{\circ}$,求点$P$的坐标.

答案:
(1)由抛物线的对称性及$AB = 4$,易得$A(-2,0)$,$B(2,0)$.将$B(2,0)$代入$y = ax^{2}+4$,得$4a + 4 = 0$,解得$a = - 1$.
∴抛物线对应的函数解析式为$y = - x^{2}+4$.(2)过点C作$CD⊥AC$,交AP的延长线于点D,过点D作$DE⊥y$轴于点E.
∵$∠CAP = 45°$,$AC⊥CD$,
∴$\triangle CAD$是等腰直角三角形.
∴易得$\triangle AOC≌\triangle CED$.
∴$AO = CE$,$OC = ED$.
∴易得点D的坐标为$(4,2)$.设直线AD对应的函数解析式为$y = kx + b$.将$A(-2,0)$,$D(4,2)$代入,得$\begin{cases}-2k + b = 0\\4k + b = 2\end{cases}$,解得$\begin{cases}k = \frac{1}{3}\\b = \frac{2}{3}\end{cases}$.
∴直线AD对应的函数解析式为$y = \frac{1}{3}x + \frac{2}{3}$.令$-x^{2}+4 = \frac{1}{3}x + \frac{2}{3}$,解得$x_1 = - 2$,$x_2 = \frac{5}{3}$.
∵点A的坐标是$(-2,0)$,
∴点P的横坐标是$\frac{5}{3}$,
∴点P的坐标是$(\frac{5}{3},\frac{11}{9})$.
∴抛物线对应的函数解析式为$y = - x^{2}+4$.(2)过点C作$CD⊥AC$,交AP的延长线于点D,过点D作$DE⊥y$轴于点E.
∵$∠CAP = 45°$,$AC⊥CD$,
∴$\triangle CAD$是等腰直角三角形.
∴易得$\triangle AOC≌\triangle CED$.
∴$AO = CE$,$OC = ED$.
∴易得点D的坐标为$(4,2)$.设直线AD对应的函数解析式为$y = kx + b$.将$A(-2,0)$,$D(4,2)$代入,得$\begin{cases}-2k + b = 0\\4k + b = 2\end{cases}$,解得$\begin{cases}k = \frac{1}{3}\\b = \frac{2}{3}\end{cases}$.
∴直线AD对应的函数解析式为$y = \frac{1}{3}x + \frac{2}{3}$.令$-x^{2}+4 = \frac{1}{3}x + \frac{2}{3}$,解得$x_1 = - 2$,$x_2 = \frac{5}{3}$.
∵点A的坐标是$(-2,0)$,
∴点P的横坐标是$\frac{5}{3}$,
∴点P的坐标是$(\frac{5}{3},\frac{11}{9})$.
查看更多完整答案,请扫码查看


