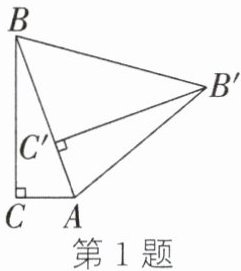
1. 如图,在Rt△ABC中,∠C= 90°,∠BAC= 70°,将△ABC绕点A按顺时针方向旋转70°,点B,C旋转后的对应点分别是B',C',连接BB',则∠B'BC'的度数为 ( )
A.35°
B.40°
C.50°
D.55°

A.35°
B.40°
C.50°
D.55°
答案:
D
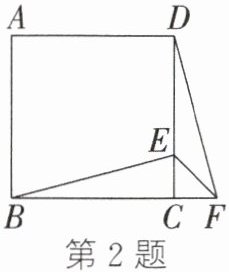
2. 如图,在正方形ABCD中,E为边CD上一点,连接BE,∠EBC= 15°,将△EBC绕点C按顺时针方向旋转90°得到△FDC,连接EF,则∠EFD的度数为 ( )
A.15°
B.20°
C.25°
D.30°

A.15°
B.20°
C.25°
D.30°
答案:
D
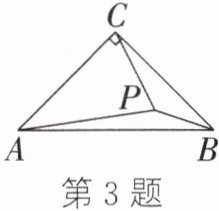
3. 如图,在等腰直角三角形ABC中,∠ACB= 90°,P为三角形内一点,且$PC= \sqrt{2}$,$PB= 1$,$PA= \sqrt{5}$,则∠BPC的度数为______.

答案:
135°
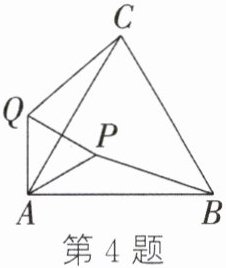
4. 如图,△ABC是等边三角形,点P在△ABC内,$PA= 2$,将△PAB绕点A按逆时针方向旋转得到△QAC,则PQ的长为 ( )
A.2
B.$\sqrt{3}$
C.$\frac{3}{2}$
D.1

A.2
B.$\sqrt{3}$
C.$\frac{3}{2}$
D.1
答案:
A
5. 如图,CD是△ABC的边AB上的中线,将线段AD绕点D按顺时针方向旋转90°后,点A的对应点E恰好落在边AC上.若$AD= \sqrt{2}$,$BC= \sqrt{5}$,则AC的长为 ( )
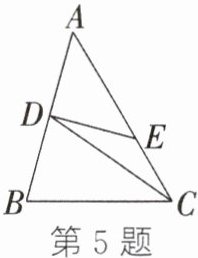
A.$\sqrt{7}$
B.3
C.$2\sqrt{3}$
D.4

A.$\sqrt{7}$
B.3
C.$2\sqrt{3}$
D.4
答案:
B
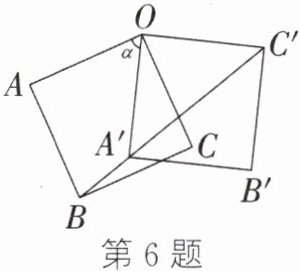
6. (2022·温岭期中)如图,正方形OABC的边长为2,将正方形OABC绕点O按逆时针方向旋转$\alpha(0°<\alpha<180°)$得到正方形OA'B'C',连接BC',则当点A'恰好落在线段BC'上时,BC'的长是______.

答案:
$\sqrt{6}+\sqrt{2}$
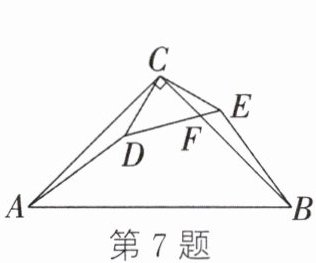
7. 如图,在Rt△ABC中,∠ACB= 90°,CA= CB= 8 cm,D为△ABC内一点,∠ACD= 15°,CD= 3 cm.连接AD,将△ACD绕点C按逆时针方向旋转,使得CA与CB重合,点D的对应点为E.连接DE交BC于点F,则BF的长为______cm.

答案:
$(8 - \sqrt{6})$ 解析:如图,过点 C 作$CG\perp DE$于点 G.
∵ 将$\triangle ACD$绕点 C 按逆时针方向旋转,使得 CA 与 CB 重合,
∴ $CD = CE$、$\angle DCE = 90^{\circ}$,$\angle BCE = \angle ACD = 15^{\circ}$.
∴ $\angle CED = \angle CDE = 45^{\circ}$.在$\triangle CEF$中,$\angle CFD = \angle CEF + \angle ECF = 45^{\circ} + 15^{\circ} = 60^{\circ}$.在$Rt\triangle CDG$中,$\angle CDG = 45^{\circ}$,$CD = 3\mathrm{cm}$,由勾股定理,易得$CG = DG = \frac{3\sqrt{2}}{2}\mathrm{cm}$.在$Rt\triangle CFG$中,$\angle CFG = 60^{\circ}$,$CG = \frac{3\sqrt{2}}{2}\mathrm{cm}$,由勾股定理,易得$GF = \frac{\sqrt{6}}{2}\mathrm{cm}$.
∴ $CF = 2GF = \sqrt{6}\mathrm{cm}$.
∴ $BF = CB - CF = (8 - \sqrt{6})\mathrm{cm}$.
∵ 将$\triangle ACD$绕点 C 按逆时针方向旋转,使得 CA 与 CB 重合,
∴ $CD = CE$、$\angle DCE = 90^{\circ}$,$\angle BCE = \angle ACD = 15^{\circ}$.
∴ $\angle CED = \angle CDE = 45^{\circ}$.在$\triangle CEF$中,$\angle CFD = \angle CEF + \angle ECF = 45^{\circ} + 15^{\circ} = 60^{\circ}$.在$Rt\triangle CDG$中,$\angle CDG = 45^{\circ}$,$CD = 3\mathrm{cm}$,由勾股定理,易得$CG = DG = \frac{3\sqrt{2}}{2}\mathrm{cm}$.在$Rt\triangle CFG$中,$\angle CFG = 60^{\circ}$,$CG = \frac{3\sqrt{2}}{2}\mathrm{cm}$,由勾股定理,易得$GF = \frac{\sqrt{6}}{2}\mathrm{cm}$.
∴ $CF = 2GF = \sqrt{6}\mathrm{cm}$.
∴ $BF = CB - CF = (8 - \sqrt{6})\mathrm{cm}$.
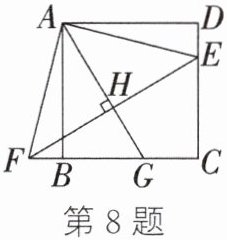
8. 如图,点E在正方形ABCD的边CD上.将△ADE绕点A按顺时针方向旋转90°到△ABF的位置,连接EF,过点A作AG⊥EF于点H,交BC于点G.若BG= 3,CG= 2,则CE的长为______.

答案:
$\frac{15}{4}$ 解析:如图,连接 EG.由题意,可知$\triangle ADE\cong\triangle ABF$,
∴ $AE = AF$,$DE = BF$.又
∵ $AG\perp EF$,
∴ H 为 EF 的中点,
∴ AG 垂直平分 EF.
∴ $EG = FG$.易知正方形 ABCD 的边长为$3 + 2 = 5$.设$CE = x$,则$DE = BF = 5 - x$.
∴ $FG = BF + BG = 8 - x$.
∴ $EG = 8 - x$.
∵ $\angle C = 90^{\circ}$,
∴ 在$Rt\triangle CEG$中,$CE^{2} + CG^{2} = EG^{2}$,即$x^{2} + 2^{2} = (8 - x)^{2}$,解得$x = \frac{15}{4}$.
∴ CE 的长为$\frac{15}{4}$.
∴ $AE = AF$,$DE = BF$.又
∵ $AG\perp EF$,
∴ H 为 EF 的中点,
∴ AG 垂直平分 EF.
∴ $EG = FG$.易知正方形 ABCD 的边长为$3 + 2 = 5$.设$CE = x$,则$DE = BF = 5 - x$.
∴ $FG = BF + BG = 8 - x$.
∴ $EG = 8 - x$.
∵ $\angle C = 90^{\circ}$,
∴ 在$Rt\triangle CEG$中,$CE^{2} + CG^{2} = EG^{2}$,即$x^{2} + 2^{2} = (8 - x)^{2}$,解得$x = \frac{15}{4}$.
∴ CE 的长为$\frac{15}{4}$.
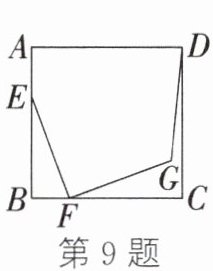
9. 如图,在正方形ABCD中,AB= 4,点E在边AB上,点F在边BC上,且BF= 1.连接EF,将线段EF绕点F按顺时针方向旋转90°得到线段GF,连接DG,则DG长的最小值为 ( )
A.2
B.$2\sqrt{2}$
C.3
D.$\sqrt{10}$

A.2
B.$2\sqrt{2}$
C.3
D.$\sqrt{10}$
答案:
C
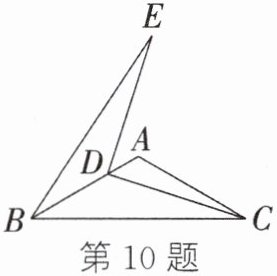
10. (2023·温岭期中)如图,在△ABC中,∠BAC= 120°,AB= AC= 6,D为边AB上一动点(不与点B重合),连接CD,将线段CD绕点D按逆时针方向旋转90°得到线段ED,连接BE,则$S_{\triangle BDE}$的最大值为______.

答案:
$\frac{81}{8}$
查看更多完整答案,请扫码查看


